grad, div, rotの高校数学っぽい解説【物理】

大学物理の1年生で習う電磁気学で、\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)というモノが登場します。
(\(\mathrm{grad}\)、\(\mathrm{rot}\)は力学でもちょっと出てくる。)

これらはいわばベクトル微分トリオです。
トリオで登場するやつらという意味では\(\mathrm{sin}\)、\(\mathrm{cos}\)、\(\mathrm{tan}\) (三角関数トリオ) と似ています。

高校数学では\(\mathrm{sin}\)、\(\mathrm{cos}\)、\(\mathrm{tan}\)については相当みっちり習いましたよね。
だからみんなある程度使いこなせるようになってるはずです。

ところがブログ主が大学生だったとき、\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)については大学の教授先生はあんまり詳しく説明をしてくれませんでした。

大学によっては詳しく教えてくれる先生もいるかもしれませんが、少なくとも高校の\(\mathrm{sin}\)、\(\mathrm{cos}\)、\(\mathrm{tan}\)ほどはやっていないはずです。

そのため「\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)? はて?」という状態で講義が進んで行ってしまう人もいるのではと思います。

そこでこの記事で高校数学くらいの (せめて高校の教科書くらいの) ちゃんとした説明をしようと思います。ただしあくまで私の理解です。

\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)が登場するタイミング

物理学を習ってこの中ではじめに出てくるのは、おそらく\(\mathrm{grad}\)だと思います。

力学で、ポテンシャルエネルギーと力の関係を表す式として出てきます。

ポテンシャルの勾配と力

ベクトルである次のような微分演算子\(\mathrm{grad}\) (読み方: グラディエント)
\(\mathrm{grad}=\displaystyle\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right)\tag{1}\)
を定義すると、力 (保存力) \(\vec{F}\)とポテンシャル\(U(\vec{r})\)との関係は、
\(\vec{F}=-\mathrm{grad}U\tag{2}\)
と表される。
\(\mathrm{grad}U(\vec{r})\)は位置の関数\(U(\vec{r})\)の勾配を表している。

(ブログ主が作成した文章です)

保存力とかポテンシャルとかいうワードは今はとくに意味がわからなくても大丈夫です。
(「保存力」というワードについてはもしよかったらこちらの記事も参照してみてください。)

そして「勾配」というキーワードが重要なので赤字にしておきました。

また、\(\mathrm{grad}\)は微分演算子なんだな、ということも書いてありますね。

次に出てくるタイミングは、\(\mathrm{grad}\)の少し後で、力学で\(\mathrm{rot}\)が登場するかもしれません。
ただし、先生によっては力学で\(\mathrm{rot}\)の話はしないかもしれません。その場合は電磁気学ではじめて出てくると思います。

力学で出てくるなら、下記のように、力が保存力であるための条件式として出てくると思います。

力が保存力であることの条件

\(\mathrm{rot}\) (読み方: ローテーション) は微分演算子であり、次式を表す。
\(\mathrm{rot}\vec{F}=\displaystyle\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}, \frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\tag{3}\)
力\(\vec{F}\)が保存力であることと次式は同値である。
\(\mathrm{rot}\vec{F}=\vec{0}\tag{4}\)
\(\mathrm{rot}\vec{F}\)は位置\(\vec{r}\)におけるベクトル場\(F(\vec{r})\)の回転を表す量である。

(ブログ主が作成した文章です)

ここも保存力というワードはわからなくても大丈夫です。

そして「回転」というキーワードが重要なので赤字にしておきました。

また、\(\mathrm{rot}\)も\(\mathrm{grad}\)と同じく微分演算子なんだな、ということも書いてありますね。

つぎに、\(\mathrm{rot}\)が電磁気学で出てくる場合は、下記のような感じだと思います。

電場の渦なしの法則

静電場\(\vec{E}(\vec{r})\)と電位\(V(\vec{r})\)の関係は
\(\vec{E}(\vec{r})=-\mathrm{grad}V(\vec{r})\tag{5}\)
である。これに
\(\mathrm{rot}(\mathrm{grad}\vec{A})=\vec{0}\tag{6}\)
という公式を使えば、静電場の渦なしの法則
\(\mathrm{rot}\vec{E}(\vec{r})=\vec{0}\tag{7}\)
が得られる。

(ブログ主が作成した文章です)

渦なしの法則、電場、電位 というワードはわからなくても大丈夫です。

上記の文章には、\(\mathrm{rot}(\mathrm{grad}\vec{A})=\vec{0}\)という一般的に成り立つ公式があるらしいことも書かれています。

最後に、\(\mathrm{div}\)が電磁気学で登場すると思います。

ガウスの法則の微分形

\(\mathrm{div}\) (読み方: ダイバージェンス) は発散 (湧き出しともいう) を表す微分演算子であり、次式を表す。
\(\mathrm{div}\vec{A}=\displaystyle\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\tag{8}\)
電場\(\vec{E}(\vec{r})\)について、一般的に、電荷密度を\(\rho(\vec{r})\)、透磁率を\(\epsilon_0\)とすると、
\(\mathrm{div}\vec{E}(\vec{r})=\displaystyle\frac{\rho(\vec{r})}{\epsilon_0}\tag{9}\)
が成り立つ。これをガウスの法則の微分形といい、マクスウェル方程式の1つである。

(ブログ主が作成した文章です)

ガウスの法則、微分形、電場、電荷密度、透磁率、マクスウェル方程式 というワードはわからなくても大丈夫です。

そして「発散 (湧き出し)」というキーワードが重要なので赤字にしておきました。
\(\mathrm{div}\)は「発散」と呼ばれることもありますし、「湧き出し」と呼ばれることもあります。
どちらでも意味は同じです。

また、\(\mathrm{div}\)も\(\mathrm{grad}\)、\(\mathrm{rot}\)と同じく微分演算子なんだな、ということも書いてありますね。

いちばん始めに覚えたいことは、「もとになる量･できる量の形式」

\(\mathrm{grad}\)は、スカラー関数にかかる演算子、\(\mathrm{div}\)、\(\mathrm{rot}\)はどちらもベクトルにかかる演算子です。

\(\mathrm{grad}\)はベクトルに作用させることはできません。

\(\mathrm{div}\)、\(\mathrm{rot}\)の2つは同じベクトル場\(\vec{A}(\vec{r})\)に作用させることが可能です。
(ベクトル場とは位置の関数になっているベクトルのことです。)

\(\mathrm{div}\)、\(\mathrm{rot}\)の2つはスカラー関数に作用させることはできません。

\(\mathrm{grad}\)がスカラー関数\(\phi(\vec{r})\) (引数の\(\vec{r}\)は以後省略することもあります) に作用した結果の物は、\(\mathrm{grad}\phi\)と書きます。

\(\mathrm{div}\)、\(\mathrm{rot}\)がベクトル\(\vec{A}\) (引数の\(\vec{r}\)は以後省略することもあります) に作用した結果の物は、\(\mathrm{div}\vec{A}\)、\(\mathrm{rot}\vec{A}\)と書きます。

演算の結果としてできる量 (の形式) は、\(\mathrm{grad}\)はベクトル、\(\mathrm{div}\)はスカラー、\(\mathrm{rot}\)はベクトルです。

以上のことをまず覚えてほしいです! (重要)

演算子	もとになる量	できる量
\(\mathrm{grad}\)	スカラー	ベクトル
\(\mathrm{div}\)	ベクトル	スカラー
\(\mathrm{rot}\)	ベクトル	ベクトル

具体的にどんな量になるのかというと、こちらの項の例文に出てきたように、下記の量になります。
(スカラー関数\(\phi\)およびベクトル\(\vec{A}=(A_x, A_y, A_z)\)に作用させた場合の例)

演算	値
\(\mathrm{grad}\phi\)	\(\displaystyle\left(\color{red}{\frac{\partial \phi}{\partial x}}, \color{blue}{\frac{\partial \phi}{\partial y}}, \color{green}{\frac{\partial \phi}{\partial z}}\right)\)
\(\mathrm{div}\vec{A}\)	\(\color{orange}{\displaystyle\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}}\)
\(\mathrm{rot}\vec{A}\)	\(\displaystyle\left(\color{red}{\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}}, \color{blue}{\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}}, \color{green}{\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}}\right)\)

わかりやすいように各要素ごとに色をつけてみました。

表1と見比べてみてください。確かに、\(\mathrm{grad}\phi\)の値はベクトル、\(\mathrm{div}\vec{A}\)の値はスカラー、\(\mathrm{rot}\vec{A}\)の値はベクトル になっていることがわかるのではないでしょうか。

\(\mathrm{grad}\)の意味

\(\mathrm{grad}\phi\)はベクトル量です。
では\(\mathrm{grad}\phi\)は何を表す量なのでしょうか?

答えを言います。
\(\mathrm{grad}\phi\)は、「勾配」を表します。「勾配」というワードは例文にも出てきましたね。

「勾配」とは、いいかえれば「傾き」です。
「勾配」というイメージをつかむには、2次元の関数で考えるといいと思まいす。

2次元の場合のグラディエントは、次のようなベクトルになります。

\(\mathrm{grad}\phi=\displaystyle\left(\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}\right)\tag{10}\)

2次元スカラー場 (= 平面上の位置の関数で、戻り値がスカラー値のもの。) \(\phi(\vec{r})\)は、関数の値を\(z\)軸に取って図に書くと曲面になっているはずです。(下図の\(z=\phi(\vec{r})\)とする)

(下図はDesmosというサイトで作成した図)

曲面の中の各点(位置\(\vec{r}\))において、周囲360度のうち、「勾配」\(\mathrm{grad}\phi(\vec{r})\)の方向がもっとも傾斜が大きい方向になっています。

また、「勾配」\(\mathrm{grad}\phi\)の「大きさ」は傾斜が大きいほど大きくなります。

なぜ\(\displaystyle\left(\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}\right)\) (３次元なら、\(\displaystyle\left(\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi}{\partial z}\right)\)) という量がそのような性質を表すのかは、ここでは詳しく説明しません。
(しかし、ちゃんと説明はできます。いつか記事を書きたいです。)

とりあえず、そのような性質を持ったベクトル量だということを覚えてください。

3次元の場合でも、イメージはまったく同じです。

例1: スカラー関数\(\phi(\vec{r})=\sin{x}+\cos{y} + z\)の、点\((x, y, z)=\left(\displaystyle\frac{\pi}{2}, \frac{\pi}{6}, 2\right)\)における勾配 (グラディエント) を求めてみましょう。

\begin{eqnarray}\mathrm{grad}\phi(\vec{r})=\left(\displaystyle\frac{\partial \phi(\vec{r})}{\partial x}, \frac{\partial \phi(\vec{r})}{\partial y}, \frac{\partial \phi(\vec{r})}{\partial z}\right)\end{eqnarray}

ここで、\(\phi(\vec{r})=\sin{x}+\cos{y} + z\)より、

\begin{eqnarray}\left\{\begin{array}{l}
\displaystyle\frac{\partial \phi(\vec{r})}{\partial x}=\cos{x}\\
\displaystyle\frac{\partial \phi(\vec{r})}{\partial y}=-\sin{y}\\
\displaystyle\frac{\partial \phi(\vec{r})}{\partial z}=1
\end{array}\right.\end{eqnarray}

なので、

\begin{eqnarray}\mathrm{grad}\phi(\vec{r})=\left(\cos{x}, -\sin{y}, 1\right)\end{eqnarray}

したがって点\((x, y, z)=\left(\displaystyle\frac{\pi}{2}, \frac{\pi}{6}, 2\right)\)では、

\begin{eqnarray}\mathrm{grad}\phi(\vec{r})&=&\displaystyle\left(\cos{\frac{\pi}{2}}, -\sin{\frac{\pi}{6}}, 1\right)\\
&=&\left(0, -\displaystyle\frac{1}{2}, 1\right)\end{eqnarray}

なので点\(\displaystyle\left(\frac{\pi}{2}, \frac{\pi}{6}, 2\right)\)からみたらベクトル\(\left(0, -\displaystyle\frac{1}{2}, 1\right)\)の方向がいちばん関数\(\phi\)の増加が大きいということになります。
また、\(\mathrm{grad}\phi(\vec{r})\)の大きさは

\begin{eqnarray}|\mathrm{grad}\phi(\vec{r})|&=&\sqrt{0^2+\left(-\displaystyle\frac{1}{2}\right)^2+1^2}\\
&=&\displaystyle\frac{\sqrt{5}}{2}\end{eqnarray}

なのでその方向の関数の傾き(= 値の変化率)は\(\displaystyle\frac{\sqrt{5}}{2}\)だということがわかります。

\(\mathrm{div}\)の意味

\(\mathrm{div}\vec{A}\)はスカラー量です。
では\(\mathrm{div}\vec{A}\)は何を表す量なのでしょうか?

答えを言います。
\(\mathrm{div}\vec{A}\)は、「湧き出し」を表します。(または「発散」ともいいますが、「湧き出し」のほうがイメージしやすいと思います。)
「湧き出し(発散)」というワードは例文にも出てきましたね。

たとえば、下図のようなベクトル場\(\vec{A}(\vec{r})\)があったとします。

まず、図(A)に注目してください。

全域で同じ大きさのベクトル場となっています。
これは「湧き出しの無い」ベクトル場です。

次に、図(B)に注目してください。

赤色のあたりでベクトルの大きさが大きくなっている様子が見受けられます。
まるで、水の流れでいうと、赤色のところで水流が湧き出ているために、それより右の部分は流れが強くなっているような様子です。

このように、ベクトル場中でベクトルの大きさが増えているということを、「湧き出しのある」ベクトル場といいます。

このような「湧き出しのある」場所において、\(\mathrm{div}\vec{A}(\vec{r})\)の値は\(0\)以外の値になります。

また、\(\mathrm{div}\vec{A}(\vec{r})\)の「大きさ」は、位置\(\vec{r}\)における湧き出しが強いほど大きくなります。

なぜ\(\displaystyle\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\)という量がそのような性質を表すのかは、ここでは詳しく説明しません。
(しかし、ちゃんと説明はできます。いつか記事を書きたいです。)

とりあえず、そのような性質を持ったベクトル量だということを覚えてください。

上の図は2次元風の図ですが、3次元の場合でも、イメージはまったく同じです。

例2: ベクトル場\(\vec{A}(\vec{r})=(2x, xy, x+z)\)の、点\((x, y, z)=(1, 2, 3)\)における湧き出し (ダイバージェンス) を求めてみましょう。

\begin{eqnarray}\mathrm{div}\vec{A}(\vec{r})=\displaystyle\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\end{eqnarray}

ここで、\(\vec{A}(\vec{r})=(2x, xy, x+z)\)より、

\begin{eqnarray}
\mathrm{div}\vec{A}(\vec{r})&=&\displaystyle\frac{\partial}{\partial x}(2x) + \frac{\partial}{\partial y}(xy) + \frac{\partial}{\partial z}(x+z)\\
&=&2+x+1\\
&=&x+3
\end{eqnarray}

したがって点\((x, y, z)=(1, 2, 3)\)では、

\begin{eqnarray}
\mathrm{div}\vec{A}(\vec{r})&=&1+3\\
&=&4
\end{eqnarray}

なので点\((x, y, z)=(1, 2, 3)\)では湧き出しがあり、湧き出しの強さは\(4\)です。
ちなみに点\((x, y, z)=(2, 2, 3)\)では、

\begin{eqnarray}
\mathrm{div}\vec{A}(\vec{r})&=&2+3\\
&=&5
\end{eqnarray}

なので点\((x, y, z)=(2, 2, 3)\)でも湧き出しがあり、湧き出しの強さは\(5\)です。

なので点\((x, y, z)=(1, 2, 3)\)よりも点\((x, y, z)=(2, 2, 3)\)でのほうが湧き出しは強いということです。

さらに、点\((x, y, z)=(-5, 0, 0)\)では、

\begin{eqnarray}
\mathrm{div}\vec{A}(\vec{r})&=&-5+3\\
&=&-2
\end{eqnarray}

なので点\((x, y, z)=(-5, 0, 0)\)の湧き出しは\(-2\) (= 負)です。
マイナスの湧き出しは吸い込み (ブログ主が今作った表現で正式な名称ではないので注意) を表します。この点でベクトルの大きさが小さくなるということを意味します。

\(\mathrm{rot}\)の意味

\(\mathrm{rot}\vec{A}\)はベクトル量です。
では\(\mathrm{rot}\vec{A}\)は何を表す量なのでしょうか?

答えを言います。
\(\mathrm{rot}\vec{A}\)は、「回転」を表します。
「回転」というワードは例文にも出てきましたね。

たとえば、下図のようなベクトル場\(\vec{A}(\vec{r})\)があったとします。

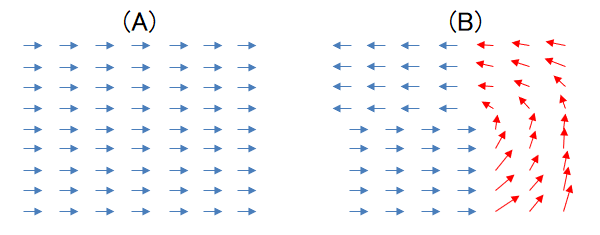
まず、図(A)に注目してください。

全域で同じ向きのベクトル場となっています。
これは「回転の無い」ベクトル場です。

次に、図(B)に注目してください。

赤色のあたりでベクトルの向きが変わっている様子が見受けられます。
まるで、水の流れでいうと、赤色のところで水流が回転して (渦巻いて) いるために、それより先の部分は流れの向きが変化しているような様子です。

このように、ベクトル場中でベクトルの向きが変化しているということを、「回転のある」ベクトル場といいます。

このような「回転のある」場所において、\(\mathrm{rot}\vec{A}(\vec{r})\)の値は\(\vec{0}\)以外の値になります。

また、\(\mathrm{rot}\vec{A}\)は、\(\mathrm{div}\vec{A}\)とちがってベクトル量です。ということは「大きさ」だけでなく「向き」を持ちます。

じつは、\(\mathrm{rot}\vec{A}\)の向きにも意味があります。
なんと、\(\mathrm{rot}\vec{A}\)の向きは、必ず回転面と垂直な向きになっているのです。
(より厳密に言えば、回転の向きに右ねじを回したとき、ねじが進む方向になっています。)

\(\displaystyle\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\)というベクトルを機械的に求めるだけで、そのような向きのベクトルが求められるのです。

なぜ\(\displaystyle\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\)という量がそのような性質を表すのかは、ここでは詳しく説明しません。
(しかし、ちゃんと説明はできます。いつか記事を書きたいです。)

とりあえず、そのような性質を持ったベクトル量だということを覚えてください。

また、上の図は2次元っぽい図ですが、\(\mathrm{rot}\)は基本的に3次元で考える (使える) 演算です。上の図はイメージを分かりやすく表すため2次元っぽい図になってます。
「\(\mathrm{rot}\)は3次元空間で使う演算」と覚えておきましょう。

例3: ベクトル場\(\vec{A}(\vec{r})=(xy, x+z, y)\)の、点\((x, y, z)=(-1, 0, 1)\)における回転 (ローテーション) を求めてみましょう。

\begin{eqnarray}\mathrm{rot}\vec{A}(\vec{r})=\displaystyle\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\end{eqnarray}

ここで、\(\vec{A}(\vec{r})=(xy, x+z, y)\)より、

\begin{eqnarray}
\mathrm{rot}\vec{A}(\vec{r})&=&\displaystyle\left(\frac{\partial}{\partial y}(y)-\frac{\partial}{\partial z}(x+z), \frac{\partial}{\partial z}(xy)-\frac{\partial}{\partial x}(y), \frac{\partial}{\partial x}(x+z)-\frac{\partial}{\partial y}(xy)\right)\\
&=&(1-1, 0-0, 1-x)\\
&=&(0, 0, 1-x)
\end{eqnarray}

したがって点\((x, y, z)=(-1, 0, 1)\)では、

\begin{eqnarray}
\mathrm{rot}\vec{A}(\vec{r})&=&(0, 0, 1-(-1))\\
&=&(0, 0, 2)
\end{eqnarray}

なので、\(\mathrm{rot}\vec{A}(\vec{r})\)は、\(z\)軸正の向きの大きさ\(2\)のベクトルであることがわかります。

\(z\)軸正の向きのベクトルであるということは、回転面はそれと垂直な面なので、回転面は\(xy\)平面と平行な平面ということです。

また、点\((x, y, z)=(0, 0, 1)\)では、

\begin{eqnarray}
\mathrm{rot}\vec{A}(\vec{r})&=&(0, 0, 1-0)\\
&=&(0, 0, 1)
\end{eqnarray}

なので、\(\mathrm{rot}\vec{A}(\vec{r})\)は、\(z\)軸正の向きの大きさ\(1\)のベクトルであることがわかります。
点\((x, y, z)=(-1, 0, 1)\)では\(|\mathrm{rot}\vec{A}|=2\)、点\((x, y, z)=(0, 0, 1)\)では\(|\mathrm{rot}\vec{A}|=1\)なので、点\((x, y, z)=(-1, 0, 1)\)でのほうが点\((x, y, z)=(0, 0, 1)\)よりも回転が強いということがわかります。(回転面の向きは同じ)

さらに、点\((x, y, z)=(2, 0, 1)\)では、

\begin{eqnarray}
\mathrm{rot}\vec{A}(\vec{r})&=&(0, 0, 1-2)\\
&=&(0, 0, -1)
\end{eqnarray}

なので点\((x, y, z)=(2, 0, 1)\)での回転を表すベクトルは、点\((x, y, z)=(-1, 0, 1)\)での回転を表すベクトル\((0, 0, 2)\)とは向きが逆方向です。
逆向きの回転ベクトルは回転方向が逆であることを表します。なので点\((x, y, z)=(2, 0, 1)\)での回転と点\((x, y, z)=(-1, 0, 1)\)での回転は逆向きの回転になっています。
覚えておきましょう。

\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\) の公式

\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)の表す意味について説明しましたが、もう1つ覚えておいてほしいことがあります。

それは、\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)を使った公式があるということです。
(公式の表式自体は必ずしもしっかり覚えなくてもとりあえずOK。最低限、公式があることだけは覚えてください。)

\(\mathrm{sin}\)、\(\mathrm{cos}\)、\(\mathrm{tan}\)にも、以下のような公式がありますよね。

\begin{eqnarray}
&&\sin^2{\theta}+\cos^2{\theta}=1\\
&&\tan{\theta}=\displaystyle\frac{\sin{\theta}}{\cos{\theta}}\\
&&1+\tan^2{\theta}=\displaystyle\frac{1}{\cos^2{\theta}}
\end{eqnarray}

これと同じようなノリです。

といっても、\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)で覚えといてほしい公式はとりあえず2つだけで、式の見た目も簡単です。
ずばり、下記の2つの式です。

\begin{eqnarray}
&&\mathrm{rot}(\mathrm{grad}\phi)=\vec{0}\tag{11}\\
&&\mathrm{div}(\mathrm{rot}\vec{A})=0\tag{12}
\end{eqnarray}

\((11)\)は、勾配の回転をとったものは必ず\(\vec{0}\)になることを表しています。
どんな関数\(\phi(\vec{r})\)の場合でも成り立つ恒等式です。

\((12)\)は、回転の発散をとったものは必ず\(0\)になることを表しています。
どんな関数\(\vec{A}(\vec{r})\)の場合でも成り立つ恒等式です。

上記の2つは物理を勉強し続けた場合、いずれ出会うことになる重要な論理の説明に使われます。

(ちらっとだけ言うと、\((11)\)はポテンシャルエネルギー (スカラー･ポテンシャル)を理解するために登場します。\((12)\)はベクトル･ポテンシャルという物を理解するために登場します。余談でした。)

ちなみに\((11)\)、\((12)\)の証明は、こちらの表の式を使って地道に計算すれば、特別な工夫をしなくてもできます。
計算がちょっと面倒くさいですけどもね。(余裕があったら、いつか記事に書くかも。)

さあ、ここまでで、\(\mathrm{grad}\)、\(\mathrm{div}\)、\(\mathrm{rot}\)については大事なポイントをそうとう学習できましたよ。

まとめ

ここまでにわかったことをまとめます。

記号	\(\mathrm{grad}\)	\(\mathrm{div}\)	\(\mathrm{rot}\)
読み方	グラディエント	ダイバージェンス	ローテーション
日本語名	勾配	発散 or 湧き出し	回転
もとになる量	スカラー	ベクトル	ベクトル
できる量	ベクトル	スカラー	ベクトル
値	\(\displaystyle\left(\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi}{\partial z}\right)\)	\(\displaystyle\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\)	\(\displaystyle\left(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\)
大きさの意味	勾配の大きさ	湧き出しの大きさ	回転の大きさ
向きの意味	最も勾配が大きい方向	–	回転面に垂直な方向 (回転の向きに右ねじを 回したとき、ねじが進む方向)

【公式】

• \(\mathrm{rot}(\mathrm{grad}\phi)=\vec{0}\)
• \(\mathrm{div}(\mathrm{rot}\vec{A})=0\)

以上です。
理解は深まったでしょうか? そうだったらよいのですが。

今回は以上とします。
読んでくれてありがとうございました。