この記事では、社会科学の知識が乏しいブログ主が、勝手に考えた社会科学っぽい理論を殴り書きします。
物理学関係の記事と違って信憑性は薄いのでご注意ください。
社会の中における人間の影響力について考察してみたいと思います。
今回は第3回目です。
人間の「行動」はベクトル量である
前回までは、
- ⑥影響者と被影響者で「行動」の種類は同一とする。
という条件を課して考察していました。
例えば、髪の色を染める、という行動だけに注目していた形です。
わずらわしいので、「行動の種類」を「ジャンル」とでも呼ぶことにしましょう。
今までジャンルが1つだけだったわけです。
ここで、ジャンルを1つ加えてみたらどうなるか考えてみたいです。
例えば、「ジョギングをする」というジャンルを追加してみましょう。
影響者のAさんは芸能人で、髪の色は赤色であり、毎晩ジョギングをしている、とテレビで発言したとしましょう。
被影響者のBさんはAさんを見て、極端な場合だと下記の4パターンの影響を受けることがありえます。
- Bさんは、髪の色を赤色に染め、かつ、毎晩ジョギングを始めた。
- Bさんは、髪の色を赤色に染めたが、ジョギングはいっさい始めなかった。
- Bさんは、髪の色は黒色のままだが、毎晩ジョギングを始めた。
- Bさんは、髪の色は黒色のままだし、ジョギングもいっさい始めなかった。
これを\((染髪, ジョギング)\)というベクトルと結び付けて考えてみましょう。すると、下図のように連想できるのではないでしょうか。
\((染髪, ジョギング) = (1, 1), (1, 0), (0, 1), (0, 0)\tag{1}\)
\(1\)は「完全影響」を表しているということです。
また、\(0\) (まったく影響を受けない) に今まで用語を定義していなかったですが、「零影響」とでも呼ぶことにしましょう。
上記のように、「行動」はベクトル量であると考えることができるのではないでしょうか。
ジャンルの競合
「髪を赤色に染める」というジャンルと「毎晩ジョギングをする」というジャンルとは、まったく独立に行うことが可能です。
ここがわりとポイントだと思います。
だから式\((1)\)のような4パターンの「行動ベクトル」が可能になります。
これがもし、「髪を赤色に染める」と「スキンヘッドにする」というジャンルの場合は、この2つを同時に行うことは不可能です。したがって、
\((赤染髪, スキンヘッド) = (1, 0), (0, 1), (0, 0)\tag{2}\)
という3パターンのみが可能となるでしょう。(もっとも単純化した考え方の場合ですが。)
このことを、
- 「髪を赤色に染める」というジャンルと、「毎晩ジョギングをする」というジャンルは、競合しない。
- 「髪を赤色に染める」というジャンルと、「スキンヘッドにする」というジャンルは、競合する。
と表現できるでしょう。
影響関数は行列と見ることができる
影響関数は、
\(a_B=E_{A→B}(a_A)\tag{3}\)
と書いたときの、\(E_{A→B}(a)\)のことでした。
いま、上記までの話で、「行動」\(a\)はベクトル量であるということに話が至りました。
とすると、\(\vec{a_B}=E_{A→B}(\vec{a_A})\)と書くことができ、\(E_{A→B}(\vec{a})\)は、ベクトルをベクトルに変換する関数ということになります。
ということは、この関数は、行列とみなしてよいのではないでしょうか。
つまり、
\(\vec{a_B}=E_{A→B}\vec{a_A}\tag{4}\)
と書いて、\(E_{A→B}\)が「影響行列」(= 影響関数) であるということです。
3人社会を考えてみる
ここで、次の条件について、緩めることを考えたいです。
①Aさん、Bさん の2人だけの社会を考える。
②影響は Aさん→Bさん の方向のみとする。
次のように、3人社会にしてみましょう。
①Aさん、Bさん、Cさんの3人だけの社会を考える。
②影響は Aさん→Cさん、Bさん→Cさん の方向のみとする。
影響者がAさんとBさん、被影響者がCさんというわけです。
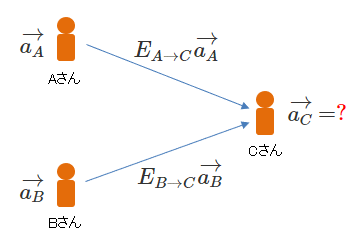
さて、この場合、Cさんの行動\(a_C\)はどうなるでしょうか。
上の図には、仮に\(E_{A→C}\vec{a_A}\)と\(E_{B→C}\vec{a_B}\)が書いてありますが、\(\vec{a_C}\)はどうなるでしょうか?
なお、\(E_{A→C}\vec{a_A}\)はAさんとCさんしかいない場合の影響、\(E_{B→C}\vec{a_B}\)はBさんとCさんしかいない場合の影響を表します。
なんとなく、\(\vec{a_C}=E_{A→C}\vec{a_A}+E_{B→C}\vec{a_B}\)となってくれると嬉しい気がしますが、そうなるでしょうか?
\(\vec{a_A}\)と\(\vec{a_B}\)が競合しない場合
\(\vec{a_A}\)と\(\vec{a_B}\)がまったく競合しない場合を考えてみましょう。
\(\vec{a_A}\)と\(\vec{a_B}\)がベクトルであることを考慮して、「競合しない」を式で表すと、次のようになるでしょう。
\( \vec{a_A}\cdot\vec{a_B}=0 \tag{3} \)
この場合を具体的な例で言うと、例えば、下記のような場合です。
(厳密に言うとわずかに競合しているかもしれませんが、まあ、今は無視して見てほしいです。)
- \(\vec{a_A}=髪を赤色に染める\)
- \(\vec{a_B}=毎晩ジョギングをする\)
この場合、\(\vec{a_C}\) (Cさんの行動) はどうなるでしょうか。
全く競合が無い場合なら、おそらく、Cさんは「髪を赤色に染める」と「毎晩ジョギングをする」の両方をするのではないでしょうか?
つまり、\(\vec{a_A}\)と\(\vec{a_B}\)がまったく競合しない場合は、
\(\vec{a_C}=E_{A→C}\vec{a_A}+E_{B→C}\vec{a_B}\tag{4}\)
が成り立っていると言えるでしょう。
\(\vec{a_A}\)と\(\vec{a_B}\)が完全に競合する場合
\(\vec{a_A}\)と\(\vec{a_B}\)が完全に競合する場合を考えてみましょう。
「完全に競合する」を式で表すと、次のようになるでしょう。
\( \vec{a_A}\cdot\vec{a_B}=\left|\vec{a_A}\right|\left|\vec{a_B}\right| \tag{5} \)
この場合を具体的な例で言うと、例えば、下記のような場合です。
- \(\vec{a_A}=髪を赤色に染める\)
- \(\vec{a_B}=スキンヘッドにする\)
この2つは絶対に両立できないです。(そういうことにしてください。)
この場合、\(\vec{a_C}\) (Cさんの行動) はどうなるでしょうか。
完全に競合する場合なら、おそらく、Cさんは「髪を赤色に染める」と「毎晩ジョギングをする」のうち、どちらか1方だけを選ぶのではないでしょうか。
では、Cさんは\(\vec{a_A}\)と\(\vec{a_B}\)のどちらを選ぶでしょうか?
これは難しい問題です。
ただ1つ言えるのは、CさんはAさんの行動\(\vec{a_A}\)とBさんの行動\(\vec{a_B}\)を見て、どちらがいいか「自分の頭で決める」でしょう。
そしてCさんの「思考」自体は表面的には現れず、「思考の結果 = 行動」だけが他者から見える形で現れると言えるのではないでしょうか。
この「思考」を「メンタル」とでも呼ぶことにします。
この「Cさんのメンタル」を\(m_C\)と表すことにしましょう。(mental のmです。)
\(m_C\)は\(\vec{a_A}\)と\(\vec{a_B}\)の関数になっているはずです。
\(\vec{m_C}=F(\vec{a_A}, \vec{a_B})\tag{6}\)
「関数」はひとまず\(F\)という記号を使っておきましたが、これに特に深い意味はありません。
そして、「メンタル」\(\vec{m_C}\)によって、「行動」\(\vec{a_C}\)が起こります。
では、「メンタル」からどのような「行動」が生まれるか?
また、完全に非競合/競合ではなく、「部分的に競合している場合」は、どのような行動が生まれるか?
これについては次回考えていきたいと思います。
今回はこのくらいにしておきます。
読んでくれてありがとうございました。
まとめ
- 人間の「行動」はベクトル量で表せる。
- 「まったく影響を受けない (=行動が変わらない)」ことを「零影響」と呼ぶことにする。
- 行動は「競合する」場合と「競合しない」場合がある。
- 行動がまったく競合しない場合を、\( \vec{a_A}\cdot\vec{a_B}=0 \)と表せる。
- 行動が完全に競合する場合を、\( \vec{a_A}\cdot\vec{a_B}=\left|\vec{a_A}\right|\left|\vec{a_B}\right| \)と表せる。
- 影響者の行動がまったく競合しない場合は、被影響者は影響者の行動をすべて同時に行うと考えられる。
- 影響者の行動が完全に競合する場合は、被影響者はまずメンタル\(\vec{m}\)に変化が起こり、それが行動\(\vec{a}\)となって表面的に表れると考えられる。
- \(\vec{m}\)は\(\vec{a_A}\)と\(\vec{a_B}\)の関数と考えられるので、\(\vec{m_C}=F(\vec{a_A}, \vec{a_B})\)と書ける。


