この記事では、社会科学の知識が乏しいブログ主が、勝手に考えた社会科学っぽい理論を殴り書きします。
物理学関係の記事と違って信憑性は薄いのでご注意ください。
社会の中における人間の影響力について考察してみたいと思います。
今回は第2回目です。
影響に制限を課す
前回の記事で、実社会における「影響力」の考察のためには下記の要考慮事項があることを述べました。
①実社会には非常に多くの人がいる
②影響は双方向に起こる
③影響力が時間にしたがって変化する
④正の影響と負の影響がある
⑤人以外からの影響がある
⑥影響者と被影響者で「行動」の種類が異なる場合がある
⑦影響が競合する可能性がある
実社会を正確に論じるためには当然、上記のすべてを考慮する必要がありますが、とても話が複雑になってしまうのでまずは単純化して考察したいです。
そこで、下記のように条件を指定してみましょう。
①Aさん、Bさん の2人だけの社会を考える。
②影響は Aさん→Bさん の方向のみとする。
③影響力は時間にしたがって変化しない。
④正の影響のみとする。
⑤人以外からの影響は無いものとする。
⑥影響者と被影響者で「行動」の種類は同一とする。
⑦ – (①、②より Aさん→Bさん の影響1つのみのため、影響の競合は考慮する必要が無い。)
もっとも単純な2人社会
上記の条件のもとでは、①②より、AさんがBさんへ一方的に影響を及ぼすことになります。
Aさんは誰からも影響を受けないので、Aさんの「行動」は変化しません。
したがってAさんの「行動」は定数ということになります。
この定数を\(c\)としましょう。
Aさんの「行動」を文字で\(a_A\)と表すことにしましょう。(action の a です。)
同時にBさんの「行動」を\(a_B\)と表すことにすると、Bさんの「行動」はAさんの「行動」の影響を受けるので、\(a_B\)は\(a_A\)の関数ということになります。
いま、Bさんの行動はAさんの行動を瞬時に反映して、まったく同じ行動をとるとしましょう。
そうすると、AさんとBさんは初期値以外はすべて同じ行動をとることになります。
Aさんの行動は定数ですから、(「行動」が実数で表せるとすると) 下図のようになります。
ただし、もともとBさんの行動は\(0\)だったとします。
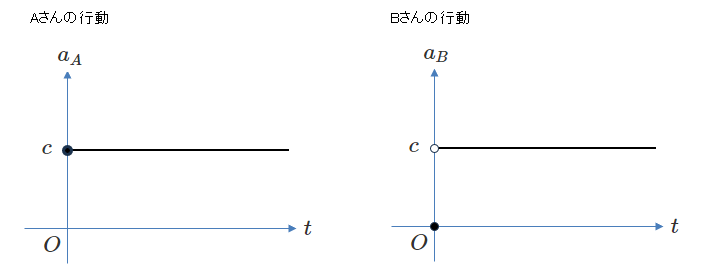
式で表すと、
\begin{eqnarray}
\left\{
\begin{array}{l}
a_A=c\\
a_B=\left\{\begin{array}{l}
0\ \ (t=0)\\
c\ \ (0<t)
\end{array}\right.
\end{array}
\right.\tag{1}
\end{eqnarray}
この単純な例では、AさんとBさんの行動が将来にわたって完全に求められました。
この例のように、被影響者が瞬時に、影響者とまったく同じ行動を取り始めることを「完全影響」とでも呼ぶことにしましょう。
逆影響
④の条件をゆるめます。
被影響者が瞬時に、影響者と逆の行動を取り始めるという現象もあると思います。
これのことを「逆影響」とでも呼ぶことにしましょう。
下図は、「完全逆影響」の図です。
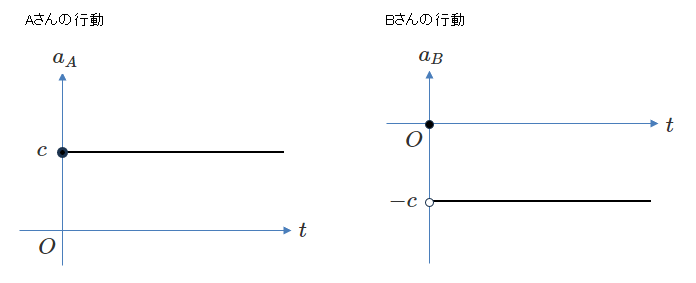
式で表すと、
\begin{eqnarray}
\left\{
\begin{array}{l}
a_A=c\\
a_B=\left\{\begin{array}{l}
0\ \ (t=0)\\
-c\ \ (0<t)
\end{array}\right.
\end{array}
\right.\tag{2}
\end{eqnarray}
影響関数
上記までの\(a_A\)と\(a_B\)の関係を、\(E_{A→B}(a)\)という関数で表すことにしましょう。
これを「影響関数」とでも呼ぶことにします。
つまり、影響関数は、
\(a_B=E_{A→B}(a_A)\tag{3}\)
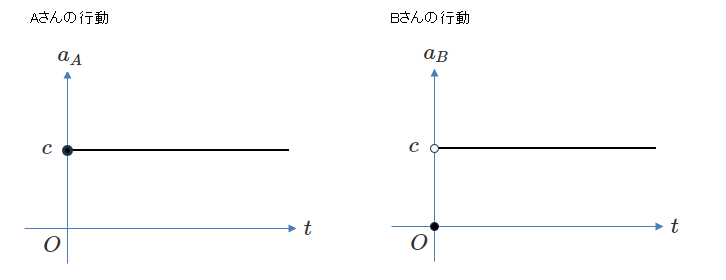
上図のような完全影響では、
\(
a_B=E_{A→B}(a_A)=\left\{
\begin{array}{l}
0\ \ (t=0)\\
a_A\ \ (0<t)
\end{array}
\right.\tag{4}
\)
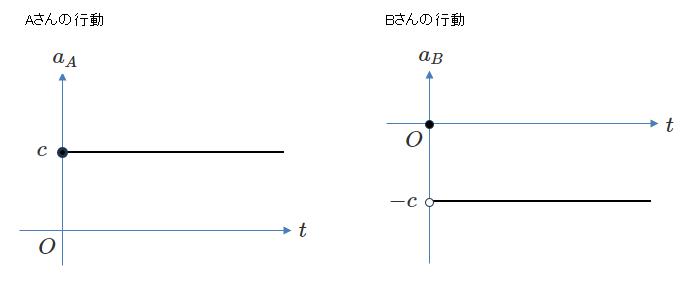
上図のような完全逆影響では、
\(
a_B=E_{A→B}(a_A)=\left\{
\begin{array}{l}
0\ \ (t=0)\\
-a_A\ \ (0<t)
\end{array}
\right.\tag{5}
\)
つまり、\(E\)の逆影響を\(Rev(E)\)と書くと、
\(E(a)=-Rev(E(a))\tag{6}\)
と書けます。
影響の大きさ
下図のBさんの行動で、グラフ1とグラフ2はどちらのほうがAさんからの影響が大きいでしょうか。

グラフ1は、Bさんの行動がAさんの行動に近づくのに長い時間がかかっていますが、最終到達点はAさんにより近いです。
グラフ2は、Bさんの行動がAさんの行動により急激に近づいていますが、最終到達点はAさんから遠いです。
どちらがAさんからの影響が大きいか、というのはどう定義するかによるだろうから、どちらでもいいといえばいいのでしょう。
しかし、ブログ主は、グラフ1のことを「小さい影響を長時間にわたって受けた」、グラフ2のことを「大きい影響を短時間にわたって受けた」と表現するのがしっくりきます。
したがって、グラフ2 (の傾きが\(0\)でない部分) のほうが大きい影響を受けたと言うことにしたいです。
そのため、「影響の大きさ = グラフの傾きの大きさ」 と定義してよいのではないでしょうか。
微分を使って表現すれば、次のようになります。
(影響の大きさを\(S(t)\)と表すことにします。)
\(S(t)=\displaystyle\frac{\mathrm{d}E(t)}{\mathrm{d}t}\tag{7}\)
「大きさ」という用語を愚直に反映すれば、次のようになりますね。
まあ、どちらでもしばらく大した問題は無いと思います。
\(S(t)=\displaystyle\left|\frac{\mathrm{d}E(t)}{\mathrm{d}t}\right|\tag{8}\)
影響関数\(E(a)\)は行動\(a\)の関数だと上では説明していましたが、\(a\)は時刻\(t\)の関数だと言えますから結局\(E(a)\)も\(t\)の関数です。
なので\(E(t)\)と書いていいはずだと思い、わかりやすいのでそうしました。
つまり、グラフ2は始めグラフ1より強い影響を受けたが、グラフ1よりも早い時刻から影響の大きさが\(0\)に変わったので、最終的に影響を長い時間受けたグラフ1のほうが到達点がAさんに近くなったという説明になります。
伝わりますでしょうか。
なおこの定義のもとでは、「完全影響」の場合は影響の大きさが\(\infty\)、「完全逆影響」の場合は影響の大きさが\(-\infty\)ということになりますね。
今回はこのへんにしたいと思います。
読んでくれてありがとうございました。
まとめ
- 「もっとも単純な2人社会」の場合なら、AさんとBさんの「行動」が将来にわたって完全に定められた。(ごく単純な場合なら、「行動」を求められる。)
- 被影響者が瞬時に、影響者とまったく同じ行動を取り始めることを「完全影響」とよぶことにする。
- 被影響者が影響者と逆の行動を取り始めることを「逆影響」とよぶことにする。
- 影響者の行動と、被影響者の行動の間の関係を、「影響関数」とよぶことにし、\(E_{A→B}(a)\)のように表すことにする。
- \(E\)の逆影響を\(Rev(E)\)と書くと、\(E(a)=-Rev(E(a))\)となる。
- 「影響の大きさ」\(S(t)\)を、\(S(t)=\displaystyle\frac{\mathrm{d}E(t)}{\mathrm{d}t}\)と定義する。
- 「完全影響」の場合は\(S(t)=\infty\)、「完全逆影響」の場合は\(S(t)=-\infty\)である。


