大学に入って物理の授業を受けると息をするかのように微分積分が登場します。
よって微分積分についていけなくなるとかなり厳しい状況になります。
しかし授業でも書籍でも、高校までのような丁寧な解説やフォローをあまりしてくれませんので、大学時の私のように壁に当たって苦しむ人がいると思うのです。
積分についていえばたとえば「線積分」という概念です。
この記事では大学時代の自分に教えるつもりも兼ねて、線積分についてやさしく解説することを試みます。ただし例によってあくまで私の理解です。
線積分には「スカラー関数の線積分」と「ベクトル関数の線積分」があるのですがこちらの記事では「スカラー関数の線積分」について解説をします。
「ベクトル関数の線積分」についてはまた改めて記事を書きたいと思っています。
高校時代の自分の積分理解「積分 = 微分の逆演算」
高校の数学で微積分については習います。
しかし学生のモチベーションとしては、受験を突破することが (=受験問題を解けることが)ほぼ唯一の目標ですので、おのずと計算能力に重きを置いた理解となります。
そうすると、積分を計算するためには「積分 = 微分の逆演算」という理解だけで、ほぼ乗り切れてしまうので、高校時代の自分はそれ以上の理解をしようともしませんでした。
\(\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(x^2)=2x\ \ \ \longleftrightarrow\ \ \ \displaystyle\int 2x \mathrm{d}x=x^2+C\tag{1}\)
\(\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(\log{x})=\displaystyle\frac{1}{x}\ \ \ \longleftrightarrow\ \ \ \displaystyle\int\displaystyle\frac{1}{x}\mathrm{d}x=\log{x}+C\tag{2}\)
「\(\displaystyle\int\ \ \ \mathrm{d}x\) は、微分の逆演算をしろという記号だ。」という理解です。
これらに挟まれたものは即座に微分の逆演算をほどこされる、それ以上の意味は無い、と。
そして、末尾の「\(\mathrm{d}x\)」は「\(x\)が積分変数である」という意味という理解です。
大学ではそれだけだと対処できない
しかし大学物理の力学では線積分という概念が出てきて、「積分 = 微分の逆演算」という理解だけだとつまずく可能性があります。
(ブログ主はつまづきました。)
下記のような文章が教科書に、不意に登場します。
[文章A]スカラー場\(\rho(x, y)\)がある。
(ブログ主が作成した文章です)
点A, 点B をむすぶ曲線Cに沿って、点Aから点Bまで\(\rho(x, y)\)を線積分した値を、
\(\displaystyle\int^{B}_{A} \rho(x, y) \mathrm{d}s\tag{3}\)
と書き表す。
ここで\(\mathrm{d}s\)は曲線C上の微小な線素である。
「曲線Cに沿って」積分するというなにやらわからない言葉が登場しました。
積分 = 微分の逆演算 でしかないのなら、「曲線に沿って」微分の逆演算するもへったくれもないわけです。
何を「曲線に沿って」行えというのでしょうか?
また、「\(\mathrm{d}s\)は曲線C上の微小な線素である。」というのもどういうことでしょうか?
「\(\displaystyle\int\ \ \ \mathrm{d}s\)」の「\(\mathrm{d}s\)」の部分は「\(s\)が積分変数である」という意味の記号で、微小な線素などというよくわからない物とは無関係なのでは?
また、被積分関数\(\rho(x, y)\)が\(s\)の関数ではないのも気になります。これでは積分計算ができません。
今回の記事では、上記の[文章A]を理解できるようになることが目標です。
ぜひ最後まで読んでみてください。
また、[文章A]を理解した結果、次のような問題が解けるようになる予定です。
お楽しみに。
[問題B]
2次元座標平面上にスカラー場\(\rho(x, y)=xy\)と曲線C: \(y=x^4\)がある。
(ブログ主が作成した文章です)
点A\((0, 0)\), 点B\((1, 1)\) をむすぶ曲線Cに沿って、点Aから点Bまで\(\rho(x, y)\)を線積分した値\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)を求めよ。
ここで\(\mathrm{d}s\)は曲線C上の微小な線素である。
「曲線Cに沿って」積分するとはどういうことか
まずは、「曲線に沿って積分する」とはどういうことかハッキリさせましょう。
ずばり言います。
「曲線に沿って積分する」とは、「曲線の式を満たしながら積分する」という意味です!
どういうことか深掘りします。
高校の積分では、たとえば「\(\displaystyle\int^{b}_{a}g(x)\mathrm{d}x\)」という積分のことを「関数\(g(x)\)を\(x=a\)から\(x=b\)まで積分する」と言ったり読んだりしますよね。
一方、今回の[文章A]では、積分の式は「\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)」となっています。
上記と一緒の考え方をして表現すると、「関数\(\rho(x, y)\)を点Aから点Bまで積分する」となります。
点Aから点Bまでの経路は無限にあります。しかし[文章A]のなかで「曲線Cに沿って」積分すると書かれています。
つまり曲線Cの方程式が\(y=f(x)\)であるとすると、「曲線Cに沿って積分する」=「\(y=f(x)\)を満たしながら積分する」ということなのです。
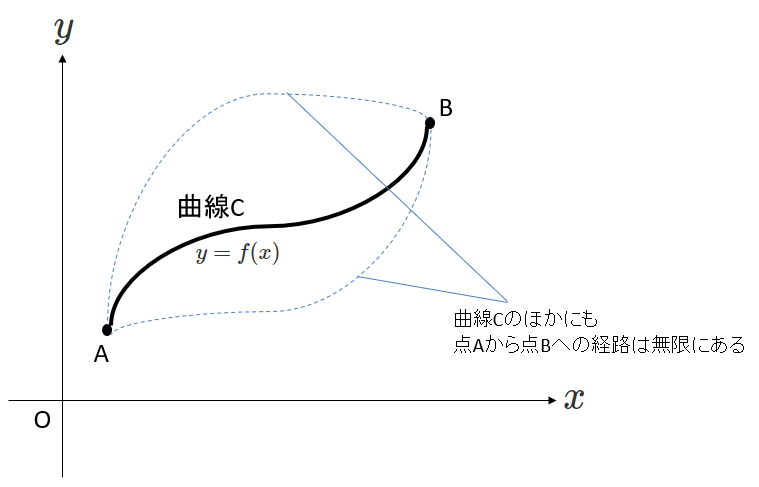
\(\rho(x, y)\)は\(x\)と\(y\)の2変数関数ですが、曲線C上では、\(y=f(x)\)が成り立ちますから、\(\rho(x, y)=\rho(x, f(x))\)と表せます。
つまり、曲線C上では\(\rho(x, y)\)は実質\(x\)の1変数関数になっているということができます。
とにかく、「曲線に沿って積分する」=「曲線の式を満たしながら積分する」と考えるようにしてください。
「\(\mathrm{d}s\)は曲線C上の微小な線素である」とはどういうことか
では「\(\mathrm{d}s\)は曲線C上の微小な線素である」とはどういうことでしょうか。
これについてはちょっと話すと長くなります。
そのため詳しいことは後日話すことにして、取り急ぎの方法を教えます。
ずばり、「\(\mathrm{d}s\)は曲線C上の微小な線素である」という言葉が出てきたら、そこを「\(s\)は曲線C上における、始点からの距離である」と読み換えてください。
始点というのは積分の始点となる点です。
今回は\(\displaystyle\int^{B}_{A}\)となっているので始点が点A、終点が点Bです。
つまり「\(s\)は曲線C上における、点Aからの距離」です。
[文章A’]スカラー場\(\rho(x, y)\)がある。
(ブログ主が作成した文章です)
点A, 点B をむすぶ曲線Cに沿って、点Aから点Bまで\(\rho(x, y)\)を線積分した値を、
\(\displaystyle\int^{B}_{A} \rho(x, y) \mathrm{d}s\tag{3}\)
と書き表す。
ここで\(s\)は曲線C上における、始点からの距離である。
積分範囲にも注目してみましょう。
\(\displaystyle\int^{B}_{A}\)となっていて、点Aが始点です。
\(s\)は曲線C上における、始点(点A)からの距離ですから、点Aにおいては\(s=0\)です。
また、曲線C上での点A~点B間の長さを\(L\)とでもおきましょう。
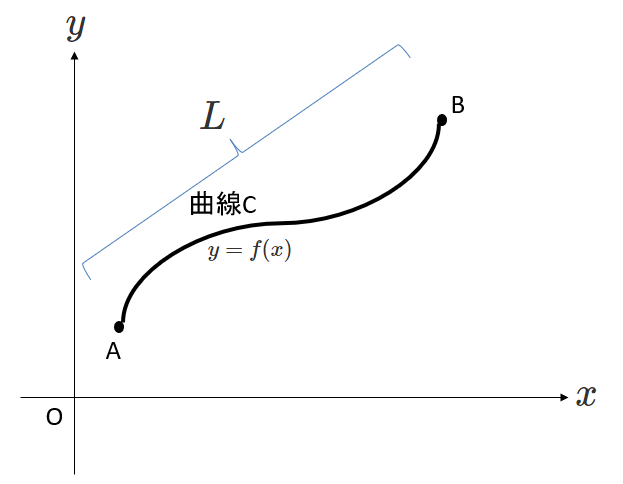
すると、「\(\displaystyle\int^{B}_{A}\ \ \ ds\)」は「\(\displaystyle\int^{L}_{0}\ \ \ \mathrm{d}s\)」とも表せます。
つまり、
\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s=\int^{L}_{0}\rho(x, y)\mathrm{d}s\tag{4}\)
です。
すなわち、\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)は、「関数\(\rho(x, y)\)を\(s=0\)から\(s=L\)まで積分せよ」という意味ということができます。
「点Aからの長さ\(s\)」が積分変数というわけです。
これで「実際に積分ができそうな形」に、徐々に近づいてきましたよ。
\(\rho(x, y)\)が\(s\)の関数じゃないから積分できない?
でも、まだ、被積分関数\(\rho(x, y)\)が\(x\)と\(y\)の関数で、積分変数\(s\)の関数ではないから、積分できないように思えます。
しかし、「被積分関数\(\rho(x, y)\)が\(s\)の関数ではない」、本当にそうでしょうか?
見た目上はたしかに\(\rho(x, y)\)というように引数が\((x, y)\)となっていて、\(s\)が関数の引数として書かれていません。
でも、曲線C上において、現実問題、\(s\)の値が決まったとき、\(x\)と\(y\)の値も決まりますよね。
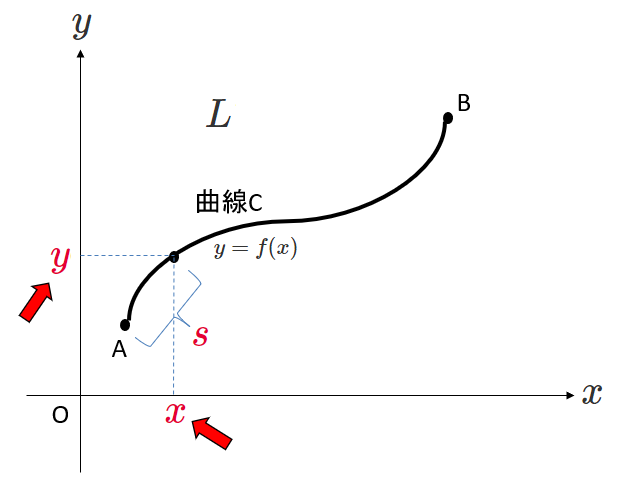
ということは、実際、\(x\)と\(y\)は\(s\)の関数で、つまり\(x\)と\(y\)の関数である\(\rho(x, y)\)も実はやっぱり\(s\)の関数なんです。
逆に考えれば\(s\)は\(x\)と\(y\)の関数だと言うこともできますね。
そして、曲線の長さ(\(s\))を求める(\(x\)の式で表す)方法は高校の数学Ⅲで習うようです。
(ブログ主は正直習った記憶が無い。でも高校数学の教科書を見たら書いてあったのでブログ主が忘れただけ??)
\(s=\displaystyle\int^{x}_{0}\sqrt{1+\left\{\displaystyle\frac{\mathrm{d}f(t)}{\mathrm{d}t}\right\}^2}\mathrm{d}t\tag{5}\)
\(x\)で微分した形は、
\(\displaystyle\frac{\mathrm{d}s}{\mathrm{d}x}=\sqrt{1+\left\{\displaystyle\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right\}^2}\tag{6}\)
です。
点Bの\(x\)座標を\(b\)とおけば、結局、上記の式\((6)\)と式\((4)\)より、
\begin{eqnarray}\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s&=&\displaystyle\int^{L}_{0}\rho(x, y)\mathrm{d}s \\
&=&\displaystyle\int^{\color{red}{b}}_{\color{red}{0}}\rho(x, y)\displaystyle\frac{\mathrm{d}s}{\color{red}{\mathrm{d}x}}\color{red}{\mathrm{d}x}\\
&=&\displaystyle\int^{b}_{0}\rho(x, y)\displaystyle\color{red}{\sqrt{1+\left\{\displaystyle\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right\}^2}}\mathrm{d}x \\ \end{eqnarray}
曲線C上では\(y=f(x)\)ですから、
\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s=\displaystyle\int^{b}_{0}\rho(x, \color{red}{f(x)})\displaystyle\sqrt{1+\left\{\displaystyle\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right\}^2}\mathrm{d}x\tag{7}\)
被積分関数が\(x\)だけの式で表せました。
この形なら、\(x\)の関数\(\rho(x, f(x))\displaystyle\sqrt{1+\left\{\displaystyle\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right\}^2}\)を\(x\)で積分すればよいのですから、計算ができますよ!
ここまでの整理
- 「曲線に沿って積分する」とはどういうことか → 曲線の式を満たしながら積分する」という意味。
- 「\(\mathrm{d}s\)は曲線C上の微小な線素である」とはどういうことか → (詳しくは説明しないが)「\(s\)は曲線C上における、始点からの距離である」と読み換える。
- \(\rho(x,y)\) が\(s\)の関数じゃないから積分できない? → 曲線の方程式によって、\(x, y\)と\(s\)は結びついているので、結局、\(\rho(x, y)\)も\(s\)の関数といえる。
(そして\(s\)も\(x\)の関数として表せる。)
さあ、満を持して、[問題B]にチャレンジしてみましょう。
問題に挑戦
[問題B]を再掲します。[問題B]
2次元座標平面上にスカラー場\(\rho(x, y)=xy\)と曲線C: \(y=x^4\)がある。
(ブログ主が作成した文章です)
点A\((0, 0)\), 点B\((1, 1)\) をむすぶ曲線Cに沿って、点Aから点Bまで\(\rho(x, y)\)を線積分した値\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)を求めよ。
ここで\(\mathrm{d}s\)は曲線C上の微小な線素である。
まず、「曲線Cに沿って線積分する」とは、「式\(y=x^4\)をみたしながら積分する」ということですね。(こちら参照)
そして、「\(\mathrm{d}s\)は曲線C上の微小な線素である。」と書いてあるので、これを「\(s\)は曲線C上における、始点からの距離である。」その\(s\)で積分するのだと、読み換えます。(こちら参照)
そして\(y=x^4\)より、
\(\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=4x^3\tag{8}\)
これを使って、高校で習った曲線の長さの求め方より、
\begin{eqnarray}s&=&\displaystyle\int^{x}_{0}\sqrt{1+(\color{red}{4t^3})^2}\mathrm{d}t\\
&=&\displaystyle\int^{x}_{0}\sqrt{1+16t^6}\mathrm{d}t\\
∴\displaystyle\frac{\mathrm{d}s}{\mathrm{d}x}&=&\sqrt{1+16x^6}\end{eqnarray}
これにより、
\begin{eqnarray}\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s&=&\displaystyle\int^{\color{red}{1}}_{\color{red}{0}}\rho(x, y)\displaystyle\frac{\mathrm{d}s}{\color{red}{\mathrm{d}x}}\color{red}{\mathrm{d}x}\\
&=&\displaystyle\int^{1}_{0}\rho(x, y)\color{red}{\sqrt{1+16x^6}}\mathrm{d}x\\
&=&\displaystyle\int^{1}_{0}\color{red}{xy}\sqrt{1+16x^6}\mathrm{d}x\\
&=&\displaystyle\int^{1}_{0}x・\color{red}{x^4}\sqrt{1+16x^6}\mathrm{d}x\\
&=&\displaystyle\int^{1}_{0}x^5\sqrt{1+16x^6}\mathrm{d}x\tag{9}\end{eqnarray}
ここで、
\(k=1+16x^6\tag{10}\)
とおくと、
\begin{eqnarray}\frac{\mathrm{d}k}{\mathrm{d}x}&=&96x^5\\
∴x^5&=&\frac{1}{96}\frac{\mathrm{d}k}{\mathrm{d}x}\tag{11}\end{eqnarray}
なので、\((9), (10), (11)\)より、
\begin{eqnarray}\require{cancel}\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s&=&\displaystyle\int^{1}_{0}\color{red}{\frac{1}{96}\frac{\mathrm{d}k}{\cancel{\mathrm{d}x}}}\sqrt{\color{red}{k}}\cancel{\mathrm{d}x}\\
&=&\displaystyle\int^{\color{red}{17}}_{\color{red}{1}}\frac{1}{96}\sqrt{k}\mathrm{d}k\\
&=&\frac{1}{96}\left[\frac{2}{3}k\sqrt{k}\right]^{17}_{1}\\
∴\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s&=&\frac{1}{144}\left(17\sqrt{17}-1\right)\end{eqnarray}
ついに、線積分\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)の値を求めることができました!
…もう少し練習したい方のために、類題をもう1つ挙げておきますね。
必要だったらチャレンジしてください。
[問題C]
2次元座標平面上にスカラー場\(\rho(x, y)=\displaystyle\frac{y}{x}\)と曲線C: \(y=\displaystyle\frac{1}{2}x^2\)がある。
(ブログ主が作成した文章です)
点A\((0, 0)\), 点B\((2, 2)\) をむすぶ曲線Cに沿って、点Aから点Bまで\(\rho(x, y)\)を線積分した値\(\displaystyle\int^{B}_{A}\rho(x, y)\mathrm{d}s\)を求めよ。
ここで\(\mathrm{d}s\)は曲線C上の微小な線素である。
読んでくれてありがとうございました。
まとめ
- 「積分 = 微分の逆演算」という理解だけだと線積分の理解に苦しむ。
- 「曲線に沿って積分する」とは、「曲線の式を満たしながら積分する」という意味。
- 「\(\mathrm{d}s\)は曲線C上の微小な線素である」という文言は「\(s\)は曲線C上における、始点からの距離である」と読み換える。
- \(\rho(x,y)\) が\(s\)の関数じゃないから積分できないように見えるが、曲線の方程式によって、\(x, y\)と\(s\)は結びついているので、結局、\(s\)も\(x\)の関数として表せる。


