大学で物理学を勉強すると力学の最初のほうで「ニュートンの運動の3法則」というものを習います。(というか高校物理でも出てくる。)
「慣性の法則」「運動の法則」「作用・反作用の法則」の3つです。
この3つのうち「慣性の法則」は「運動の法則」の言っていることに含まれており、つまり「慣性の法則」はいらないんじゃないか? ( =「運動の法則」と「作用・反作用の法則」だけでよくない? というかそれだけのほうがいいんじゃない?)
という疑問を私はかつて感じましたし、世の中にそう感じる人は多いようです。
実際「慣性の法則」はいらないのか、私なりの理解を以下で説明します。あくまで私の理解です。
なぜ疑問を感じるのか詳しくいうと
「ニュートンの運動の3法則」とは(本などによって表記は色々ですが)以下のようなものです。
ニュートンの運動の3法則
第1法則 (慣性の法則) : 静止または等速度運動している物体は、外から力が働かない場合、そのまま静止または等速度運動をつづける。
(ブログ主が作成した文です)
第2法則 (運動の法則) : 物体の加速度\( \vec{a} \)は、物体に働く力\( \vec{F} \)に比例し、物体の質量\( m \)に反比例する。(\( m\vec{a}=\vec{F} \))
第3法則 (作用・反作用の法則) : 2つの物体1, 2があって、物体1から物体2に力が働くとき、物体2は必ず物体1に対し大きさが等しく向きが反対でかつ一直線上の力を及ぼす。
ここで、第2法則にでてくる式
\( m\vec{a}=\vec{F} \tag{1} \)
は運動方程式とよばれる超重要な方程式ですが、この式から、物体に外から力が働かない場合、つまり
\( \vec{F}=\vec{0} \tag{2} \)
のとき、
\( \vec{a}=\vec{0} \tag{3} \)
であることが導かれます。\( (3) \) は加速度が\( \vec{0} \)であることを表します。加速度が\(\vec{0}\)ということはすなわち物体は静止または等速度運動をしている(しつづける)ということです。
あれ???
第2法則の式\( m\vec{a}=\vec{F} \)から、第1法則「静止または等速度運動している物体は、外から力が働かない場合、そのまま静止または等速度運動をつづける。」が導き出せてしまいました。
じゃあ第1法則いらないじゃん! 第1法則は無くして残りの2つだけで「ニュートンの運動の2法則」って呼ぶことにすれば、スッキリしててそっちのほうがいいよね?
…というのが今回の疑問の内容です。
結論を先に言うと
この問題、真剣に考えると結構難しいです。私も前に結構悩みました。
でも結論を最初に言うと「第1法則は必要」です。
安心してください。運動の法則は確かに3つ無ければ、力学を理解することは不可能なんです。
でもちょっと語弊があって、このままの言い方だと駄目なんです。正確に理解するには言い方を変える必要があります。
これからどう言えばいいのか解説していきます。
ニュートンの運動の3法則の「原理として正しい」言い方
ニュートンの運動の3法則を「原理として正しい」言い方に直したのが以下になります。
ちょっと難しいですよ。
ニュートンの運動の3法則 改
第1法則 (慣性の法則) : ある座標系で、1つの物体が「静止または等速度運動していて、外から力が働かない場合、そのまま静止または等速度運動をつづける」様子が観察されるとき、その座標系内にある他のすべての物体もまた同様に、「静止または等速度運動していて、外から力が働かない場合、そのまま静止または等速度運動をつづける」。また、座標系が加速度運動や回転をしないかぎり、その状態はいつまでもつづく。(以下この座標系を「慣性系」と呼ぶことにする。)
(ブログ主が作成した文です)
第2法則 (運動の法則) : 慣性系の中ならば例外なく、物体の加速度\( \vec{a} \)は、物体に働く力\( \vec{F} \)に比例し、物体の質量\( m \)に反比例する。(\( m\vec{a}=\vec{F} \))
第3法則 (作用・反作用の法則) : 慣性系の中ならば例外なく、「2つの物体1, 2があって、物体1から物体2に力が働くとき、物体2は必ず物体1に対し大きさが等しく向きが反対でかつ一直線上の力を及ぼす。」
お分かりになったでしょうか。(何)
赤字で書いてある部分がキモです。
これがあることによって、この3つの原理で力学のいろいろな現象をちゃんと説明できるようになりますし、これがあることによって、第1法則はやっぱり必要だといえるんです。
第1法則 (慣性の法則) について見る
第1法則 (慣性の法則) : ある座標系で、1つの物体が「静止または等速度運動していて、外から力が働かない場合、そのまま静止または等速度運動をつづける」様子が観察されるとき、その座標系内にある他のすべての物体もまた同様に、「静止または等速度運動していて、外から力が働かない場合、そのまま静止または等速度運動をつづける」。また、座標系が加速度運動や回転をしないかぎり、その状態はいつまでもつづく。(以下この座標系を「慣性系」と呼ぶことにする。)
(ブログ主が作成した文です)
これをすごく要約すると、ある座標系の中でどれか1つの物体に慣性が観察されるとき、その時点で「その座標系は慣性系です」となります。
慣性系とは、すべての物体が慣性にしたがった運動をするような座標系 (視点)です。
慣性とは、外から力が働かないかぎり,物体がそのときの運動の状態 (静止を含めた) をつづけようとする性質です。
本文の「座標系」という言葉がもしピンとこなかったら、「ある座標系で」の部分を「ある観測者から見て」と読みかえてみてください。
「系」という概念についてはこちらでも詳しめに解説してますのでよかったらご覧になってください。
(また、慣性系についてもいつか記事書きたい。重要概念なので。)
この文から読み取れることとして、「1つの物体にだけ慣性が観察され、他の物体には慣性が観察されないなどということは絶対にありません。」と、第1法則が保証してくれているということになります。
しかも座標系が加速度運動(いずれかの方向に加速する運動)や回転をしないかぎりその状態はつづくとも言っています。つまりある時から「勝手に」慣性が無くなることはありません、ということです。
ということは、実質的に「1つの物体を、今、観察しさえすれば 目の前の座標系が慣性系かどうかが分かる」ということになります。
なかなか強い宣言です。

1つの物体にだけ慣性が観察され、他の物体には慣性が観察されないなどということは絶対にありません。また座標系が加速や回転をしなければずっとその状態がつづきます。
第2法則 (運動の法則) について見る
第2法則 (運動の法則) : 慣性系の中ならば例外なく、物体の加速度\( \vec{a} \)は、物体に働く力\( \vec{F} \)に比例し、物体の質量\( m \)に反比例する。(\( m\vec{a}=\vec{F} \))
(ブログ主が作成した文です)
運動方程式(\( m\vec{a}=\vec{F} \))が、慣性系の中ならば例外なく成り立つ。
と言っていることになります。
第1法則 (慣性の法則) だけだと物体に力が働かない場合については説明しているのですが、物体に力が働く場合については何も述べていません。
そのため力を加えてみたら、物体は全部
\( m\vec{a}=2\vec{F} \tag{4} \)
に従って運動するかもしれないし、
\( m\vec{a}\cdot\vec{F}=|\vec{a}|^{2} \tag{5} \)
に従って運動するかもしれないし、
そもそも力を加えてもまったく運動が変わらないかもしれない。
それどころか物体によって\( m\vec{a}=\vec{F} \)に従って運動したり\( m\vec{a}=2\vec{F} \)に従って運動したり\( m\vec{a}=3\vec{F} \)に従って運動したりとバラバラの可能性もあります。
どの場合も、「\( \vec{F}=\vec{0} \)ならば\( \vec{a}=\vec{0} \)」は満たしていますよね。
(ぜひ確かめてみてください。)
しかし、「慣性系の中だったら絶対に全部\( m\vec{a}=\vec{F} \)に従って運動するぜ!」と、第2法則が保証してくれているということになります。
ベン図で書くと、下図の斜線部分 (慣性系だけど\( m\vec{a}=\vec{F} \)に従わない物体があるケース)は存在しないぜ! ということです。
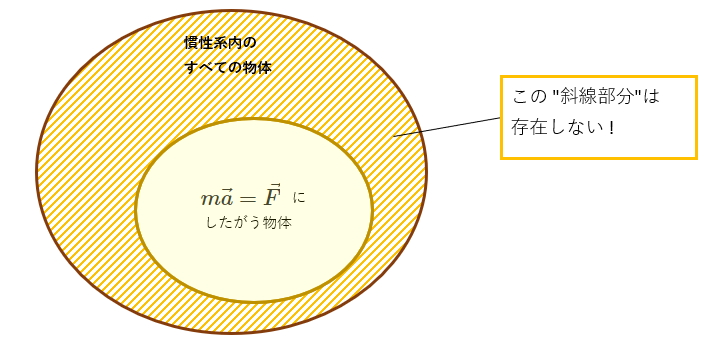

慣性系の中だったら絶対に全部\( m\vec{a}=\vec{F} \)に従って運動するぜ!!
第3法則 (作用・反作用の法則) について見る
第3法則 (作用・反作用の法則) : 慣性系の中ならば例外なく、「2つの物体1, 2があって、物体1から物体2に力が働くとき、物体2は必ず物体1に対し大きさが等しく向きが反対でかつ一直線上の力を及ぼす。」
(ブログ主が作成した文です)
これも論理構成としては第2法則と同じです。
作用・反作用のルールが、慣性系の中ならば例外なく成り立つ。
と言っていることになります。
(ここでいう「作用・反作用のルール」とは「2つの物体1, 2があって、物体1から物体2に力が働くとき、物体2は必ず物体1に対し大きさが等しく向きが反対でかつ一直線上の力を及ぼす。」のことです。)
第1法則 (慣性の法則) だけだと物体に力が働く場合については何も述べていないので、
力を加えてみたら、特定の物体にだけ反作用が働かなかったり、作用と反作用の向きが色々だったり、一直線上じゃなかったり、作用と反作用の大きさが同じじゃなかったりするかもしれません。
しかし、「慣性系の中だったら絶対に『作用・反作用のルール』が成り立つわよ!」と、第2法則が保証してくれているということになります。
ベン図で書くと、下図の斜線部分 (慣性系だけど「作用・反作用のルール」に従わない物体があるケース)は存在しないわよ! ということです。


慣性系の中だったら絶対に「作用・反作用のルール」が成り立つわよ!!
第1法則はやっぱりいる
上記までの内容を理解すれば、「第2法則は第1法則に含まれてるから不要」とは言えないです。
第2法則だけだと、「慣性系の場合→常に\( m\vec{a}=\vec{F} \)が成り立つ」ことはわかりますが、逆にいえば\( m\vec{a}=\vec{F} \)が常に成り立つためには慣性系であることを示す必要があるということです。
しかし考えてみてください。
第1法則が無い状態で、この座標系が慣性系であると判定することは事実上不可能です。
いま目の前にある物体の運動を見ただけで、「座標系内のどこに物体を置いても慣性にしたがった動きをする、しかもずっとそのままである」ことをどうして確証できるでしょう。
しかし第1法則があることによって、「”座標系内のすべての物体が常に慣性にしたがうような座標系”があって、それは1つの物体の動きを観察すれば見つけられますよ。」ということが保証されるのです。
そして、第1法則がなければ、座標系が慣性系であることの証明ができないので、第2法則と第3法則は永久に使うことができません。
第2法則の\( m\vec{a}=\vec{F} \)が使えなければ未来の物体の運動を予測することはできません。
また、第3法則が無ければ物理学で最大級に大事な法則である運動量保存の法則が導きだせません。
つまり、第1法則があるおかげで、力学の大半の理論が構築できる。
第1法則が無ければ力学の大半の理論は構築が不可能なのです。
第1法則は力学に絶対に必要なのです。
教科書の説明を見てみよう
上記までのような運動の3法則についての説明は、じつは教科書にはまったく書いてないというわけではなく、何かしら説明が書いてある教科書も結構あります。
(多くはあまり詳しく書いてない。それだけでは大学時代のブログ主には理解できなかった。)
いま、上記までの説明を読んだこの状態で、教科書に書いてある説明を見てみましょう。
●教科書① 植松恒夫 (2002年) 「力学」
(前略)
植松恒夫 (2002年) 「力学」より引用
\(m\vec{a}=\vec{F}\)とも表せる.
(中略)
\(\vec{F}=0\)のとき,
(中略)
物体は等速度運動を続けることがわかる.
それならば, 第1法則は第2法則に含まれるかというとそうではない. 第1法則は慣性の法則が成り立つ座標系すなわち慣性系 (inertial system) を設定する原理を述べており, この慣性系において第2法則が成立するのである.
「慣性系において第2法則が成立するのである」と述べられていますね。
第1法則があるからはじめて慣性系が存在することが知れて、そこで第2法則が成り立ちますよ、というニュアンスが伝わるでしょうか。
この文章から初見で正確に意味を察するのは実際にはかなり無理に近いだろうなと思います。
●教科書② 市村宗武・狩野覚 (2004年) 「大学生のための基礎シリーズ4 物理学入門 Ⅰ. 力学」
(前略)
市村宗武・狩野覚 (2004年) 「大学生のための基礎シリーズ4 物理学入門 Ⅰ. 力学」より引用
考え方を逆転させて,慣性の法則を
❝外から作用を受けていない物体が等速度直線運動をするように見える座標系が存在する❞
と言い換えよう.すなわちこの法則は先に述べた慣性の法則が成り立つ座標系の存在を主張していると理解するのである.この座標系を慣性系 (inertial system) という.
「第1法則は慣性系の存在を主張しているのだ」ということが述べられています。
つまり第1法則は第2法則に含まれることではなくまったく別のことを述べていることが示唆されています。(第2法則からは、慣性系の存在などは導けない。)
したがって第1法則は必要ですということになります。
●教科書③ 吉田弘幸 (2019年) 「はじめて学ぶ物理学 学問としての高校物理 上」
こちらの本には結構丁寧に説明してあります。せっかくなのでなるべく略さず載せます。
(下線はブログ主が引きました。)
ところで,運動方程式
\(m\vec{a}=\vec{F}\) によれば,\(\vec{F}=\vec{0}\)のとき\(\vec{a}=\vec{0}\)となる。そうすると,慣性の法則は,一見,運動方程式(運動の第2法則)の special case のように思える。しかし,もし,そうならば,慣性の法則を第1法則として掲げる意味がない。
吉田弘幸 (2019年) 「はじめて学ぶ物理学 学問としての高校物理 上」より引用
ところで,すでに学んだように加速度は観測する座標系によって値の異なる相対的な量である。したがって,外力の作用を受けない状態でも,観測する座標系に応じて加速度の値はゼロにもゼロでない値にもなる。つまり,慣性の法則は,慣性の法則が成立する座標系(これを慣性系と呼ぶ)を採用することを要請しているのである。
上で述べたように,(A)慣性の法則は我々が力学現象を観測すべき立場(観測座標系)を明示している。慣性の法則の成り立つ座標系,つまり,慣性系から観測して初めて,第2法則に従って運動方程式を書くことができるのである。ところで,慣性系は自然界に存在するのか? 日常的な現象を観測するには地面に固定した座標系が十分によい制度で慣性系と扱えることは実験的に知られている。しかし,近似的に慣性系と扱える座標系ではなく,厳密に慣性系となる座標系は本当に存在するのか? 「存在する!」ということが慣性の法則の究極的な主張である。さらに付け加えれば,(B)そのような座標系の特性は局所的なものではなく,「宇宙全体の観測について慣性の法則の成り立つ大域的な性質である」ということをも主張している。これは,(C)実験的に確かめることやほかの法則から説明することはできない要請であり,原理である。あるいは,ニュートンの哲学的自然観であると言ってもよいだろう。ニュートンは,宇宙空間に固定した座標系(絶対静止系)を慣性系の第1の候補と考えていた。
なかなかいい説明だと思います。
下線(A)の部分で、第1法則 (慣性の法則) が、第2法則 (運動方程式) を使うことが可能な座標系の条件を述べるものであることが主張されています。
下線(B)の部分で、こちらにも書いてある内容、すなわち「1つの物体に慣性が観察されるなら、他の物体にも慣性は観察されるし、座標系が移動しないかぎりこの先もずっと慣性が観察される」(= 空間・時間的に慣性系でありつづける) ことが述べられています。
下線(C)の部分で、第1法則 (慣性の法則) はやはり必要なものであることが述べられています。
最後に例題
ここまでの説明で、ニュートンの運動の3法則について少しでも理解が進んだでしょうか。
そうだったらよいのですが。
つぎの例題を見てください。
問1. つぎの文章の誤っている箇所を見つけ、訂正した文を作成せよ。
(1) ニュートンの運動の第1法則 (慣性の法則) は必要である。なぜなら、運動方程式\(m\vec{a}=\vec{F}\)を満たすが、慣性にはしたがわない物体が存在するからである。
(2) 運動方程式 (\(m\vec{a}=\vec{F}\)) と 作用・反作用のルール (2つの物体1, 2があって、物体1から物体2に力が働くとき、物体2は必ず物体1に対し大きさが等しく向きが反対でかつ一直線上の力を及ぼす) は、いついかなる場合でも成り立つ。
(3) 目の前の座標系が慣性系であるかどうか調べるためには、できうるかぎりすべての物体に慣性が観測されるかを確認しなければならないし、時間的にもずっと慣性が観測されるかを確認しなければならない。
(ブログ主が作成した文です)
まとめ
- ニュートンの運動の3法則は、よくある書き方だと「第1法則は第2法則に含まれているので不要」に見える。
- 実際はニュートンの運動の3法則をちゃんとした表記に直せば、「第1法則は必要である」といえる。
- 第1法則は、慣性系が存在し、見つけることができることを保証している。
- 運動方程式と作用・反作用のルールは、慣性系の中ならば例外なく成り立つ。慣性系でないならば成り立つ保証はない。
- 目の前にある座標系が慣性系かどうか確認するには、どれか1つの物体を観察して、慣性が観測されることを確かめるだけでよい。
以上です。読んでくれてありがとうございました。