平面極座標での速度･加速度をちゃんと理解したい【物理】

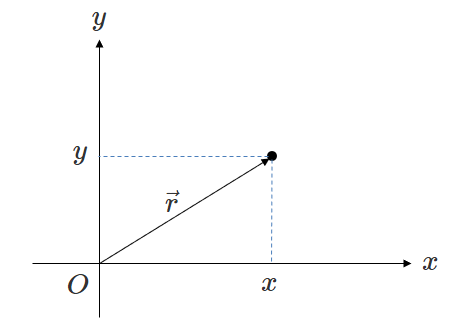
今回は極座標の話です。

大学1年生の力学の授業で、平面極座標での速度･加速度の表式について習います。
(習わない大学もあるかなあ??)

これを初めて習ったときはちょっと面食らった記憶があります。
「極座標って直交座標ほどは、単純じゃないんだなあ。」と思った感じ。
直交座標のときより複雑です。

そのちょっと複雑な表式を丸暗記する必要は、まあ、無いと思います。
現在のブログ主も暗記してないです。調べないと書けません。

ただ、速度とか、加速度とかのベクトル量が、「直交座標と極座標では表式が変わる」のだということは重要です。
この事実が座標についての理解の第1歩だからです。

もう1回言います。
ベクトル量が「直交座標と極座標では表式が変わる」ということが大事です。
具体的な表式を覚えることは重要ではありません。
上記の大事なことを心に刻むためにも、具体的な表式の求め方とかではあんまりつまづいてほしくない ので、この記事ではあえて「具体的な表式の求め方」のほうを説明したいと思います。

(求め方を見て知っておくことは有意義です。)

あくまで私の理解ですが。

速度･加速度は、「直交座標と極座標では表式が変わる」量

速度は位置を時間微分したものであり、加速度は速度を時間微分したものです。直交座標 (= \(x, y\)の文字を使った表現) では、単純に下記のようになります。

\begin{eqnarray}
速度: \left\{
\begin{array}{l}
v_x=\dot{x}\\
v_y=\dot{y}
\end{array}
\right.
\ \ \ \
加速度: \left\{
\begin{array}{l}
a_x=\ddot{x}\\
a_y=\ddot{y}
\end{array}
\right.
\end{eqnarray}

座標の\(x\)成分、\(y\)成分をそれぞれ単純に時間で微分していくだけ。
\(x\)の上のドットは「時間微分」という意味です。
つまり、\(\dot{x}\)とは\(\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}\)のことです。(\(\dot{y}\)も同様。)
そして、\(\ddot{x}\)とは\(\displaystyle\frac{\mathrm{d}^2x}{\mathrm{d}t^2}\)のことです。(\(\ddot{y}\)も同様。)

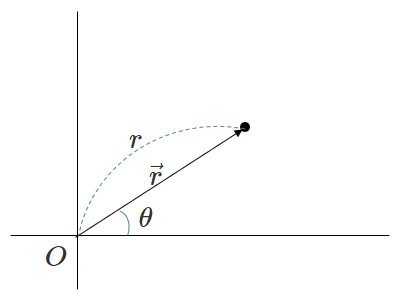
しかし、極座標 (= \(r, \theta\)の文字を使った表現) の速度･加速度は上記のように単純ではありません。
実は下記のようになります。

\begin{eqnarray}
速度: \left\{
\begin{array}{l}
v_r=\dot{r}\\
v_{\theta}=r\dot{\theta}
\end{array}
\right.
\ \ \ \
加速度: \left\{
\begin{array}{l}
a_r=\ddot{r}-r\dot{\theta}^2\\
a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}
\end{array}
\right.\tag{1}
\end{eqnarray}

なんだか複雑な式ですね。
決して、下記のようにはなりません!

\begin{eqnarray}
速度 (\color{red}{間違い!}): \left\{
\begin{array}{l}
v_r=\color{red}{\dot{r}}\\
v_{\theta}=\color{red}{\dot{\theta}}
\end{array}
\right.
\ \ \ \
加速度 (\color{red}{間違い!}): \left\{
\begin{array}{l}
a_r=\color{red}{\ddot{r}}\\
a_{\theta}=\color{red}{\ddot{\theta}}
\end{array}
\right.
\end{eqnarray}

なぜこのような表式になるのか、導いていきたいと思います。

そのために、まず、上記の\(v_r, v_{\theta}, a_r, a_{\theta}\)が図でイメージできているでしょうか?
それあたりからまず説明をしますね。

極座標の基本ベクトルは時間に依存する

直交座標系の速度の各成分\(v_x, v_y\)は、それぞれ速度ベクトル\(\vec{v}\)の\(x\)方向の成分、\(y\)方向の成分です。

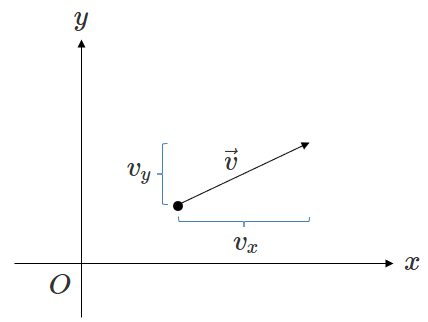
直交座標系の加速度の各成分\(a_x, a_y\)は、それぞれ加速度ベクトル\(\vec{a}\)の\(x\)方向の成分、\(y\)方向の成分です。

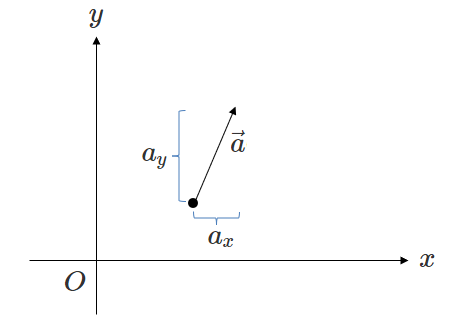
「\(x\)方向」「\(y\)方向」とはそれぞれ\(x\)軸、\(y\)軸の方向のことです。

極座標系でも、速度の各成分\(v_r, v_{\theta}\)は、それぞれ速度ベクトル\(\vec{v}\)の\(r\)方向の成分、\(\theta\)方向の成分であり、加速度の各成分\(a_r, a_{\theta}\)は、それぞれ加速度ベクトル\(\vec{a}\)の\(r\)方向の成分、\(\theta\)方向の成分です。

ただし! ここで1つ注意しておかなくてはならないことがあります。
それは「ベクトルの\(r\)方向の成分、\(\theta\)方向の成分」ってなに? ということです。

直交座標の場合はこの点が分かりやすいです。
ベクトルの\(x\)方向の成分は\(x\)軸の正の方向の成分、\(y\)方向の成分は\(y\)軸の正の方向の成分です。

なお、\(x\)方向、\(y\)方向の、大きさ\(1\)のベクトルを、ともに「基本ベクトル」と呼びます。

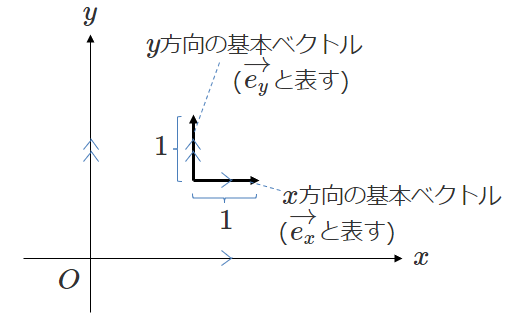
しかし極座標の場合は固定の\(r\)軸、\(\theta\)軸などというものが無いので、同じようにはいきません。

答えを言います。
じつは、\(r\)方向の基本ベクトルと、\(\theta\)方向の基本ベクトルは、「これが絶対に正しい」というものは数学的にはないです。
そのため本当は人間が自由に決めていいのですが、それでも、世界的に「これを\(r\)方向と\(\theta\)方向の基本ベクトルということにしよう」とされているものがあります。

それは、「\(r, \theta\)の値が増加するときに進む方向をそれぞれ\(r\)方向、\(\theta\)方向とと見なそう。」というものです。

「\(r\)が増加するときに進む方向」は、イコール「原点から離れる方向」です。

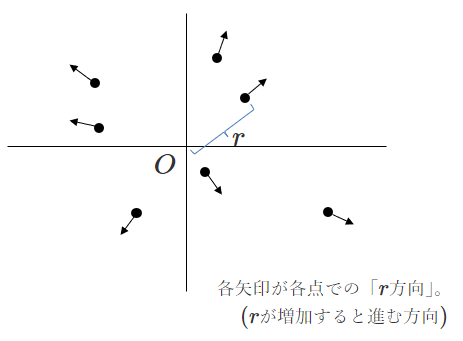
「\(\theta\)が増加するときに進む方向」は、イコール「原点から見て左回りに回る方向」です。

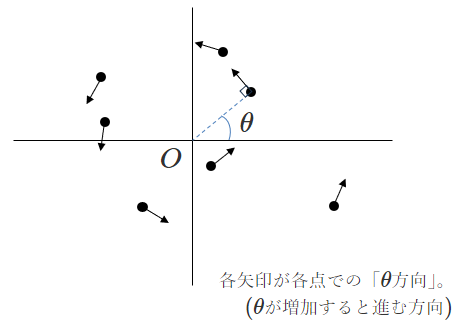
まとめて極座標の基本ベクトル\(e_r, e_{\theta}\)を図に書くと下図のようになります。

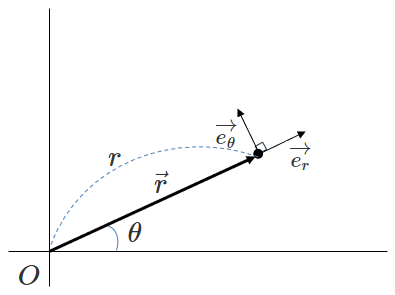
ところで、ここでさらに1つ注意が必要です。
これらの図からわかるように、「\(r\)方向」「\(\theta\)方向」にあたる方向は場所によって変わります。
なので「\(r\)方向の基本ベクトル」\(e_r\)と「\(\theta\)方向の基本ベクトル」\(e_{\theta}\)も場所によって変わります。

そして、注目している点が時間にそって運動する (= 点の位置は時間の関数である) ことにより、結局\(e_r\)と\(e_{\theta}\)は時間の関数である (\(e_r\)と\(e_{\theta}\)は時間によって変わる) ということになります。

重要なのでもう1度言います。
極座標の基本ベクトル\(e_r\)と\(e_{\theta}\)は時間の関数です!

これを覚えて先に進みましょう。

位置ベクトルを極座標表示で表すと

再度下の図を見てください。

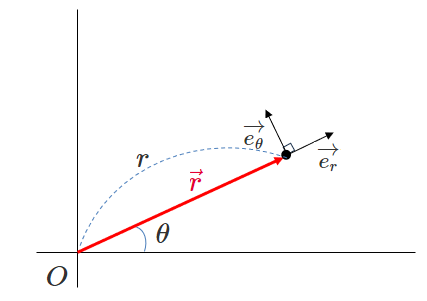
点の位置を表す位置ベクトル\(\vec{r}\)は、大きさが\(r\)で、向きが\(\vec{e_r}\)と平行です。

そのため下記のように表せます。
(基本ベクトル\(\vec{e_r}\)の大きさは\(1\)ですからね)

\(\vec{r}=r\vec{e_r}\tag{2}\)

ちなみに上の式\((2)\)はあえて下記のようにも書けます。

\(\vec{r}=r\vec{e_r}+0\vec{e_{\theta}}\tag{2′}\)

ベクトル\(\vec{r}\)の\(r\)方向 (= \(\vec{e_r}\)の方向) の大きさが\(r\)、\(\theta\)方向 (= \(\vec{e_{\theta}}\)の方向) の大きさが\(0\)ということですから、これを次のようにも表したりします。

\begin{eqnarray}
\left\{
\begin{array}{l}
r_r=r\\
r_{\theta}=0
\end{array}
\right.
\end{eqnarray}

\((2)\)を時間で微分していけば、極座標の速度、加速度が求められます。

ただし基本ベクトル\(\vec{e_r}\)も時間の関数なので、\(\vec{e_r}\)の時間微分も考える必要があります。
(基本ベクトルを時間で微分する必要があるという発想には、慣れてくださいね。)

\(\vec{e_r}\) (と、\(\vec{e_{\theta}}\)) を微分したらどうなるかをまず次に考えてみましょう。

極座標の基本ベクトルの微分

\(\vec{e_r}, \vec{e_{\theta}}\)を時間で微分するとどうなるでしょうか。

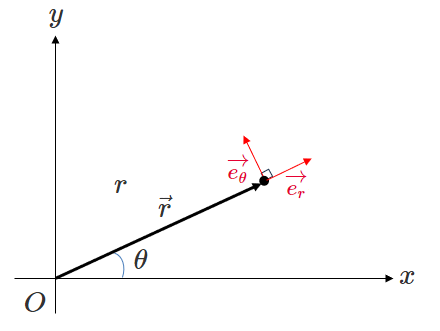
上図からわかるように、\(\vec{e_r}\)は、\(x\)軸となす角が\(\theta\)のベクトルです。
そして大きさは\(1\)です。

そして、\(\vec{e_{\theta}}\)は、\(\vec{e_r}\)を左に\(90°\)回転させた向きのベクトルです。
これも大きさは\(1\)です。

したがって、\(\vec{e_r}, \vec{e_{\theta}}\)は直交座標で表すと下記のようになります。

\begin{eqnarray}
\left\{
\begin{array}{l}
\vec{e_r}=(\cos{\theta}, \sin{\theta})\\
\vec{e_{\theta}}=(-\sin{\theta}, \cos{\theta})
\end{array}
\right.\tag{3}
\end{eqnarray}

\(\vec{e_r}\)を時間\(t\)で微分すると、(ドット「\(\dot{}\)」は時間微分を表しますからね!)

\begin{eqnarray}
\dot{\vec{e_r}}&=&\displaystyle\left(\frac{\mathrm{d}}{\mathrm{d}t}(\cos{\theta}),\frac{\mathrm{d}}{\mathrm{d}t}(\sin{\theta})\right)\\
&=&\displaystyle\left(\color{blue}{\frac{\mathrm{d}(\cos{\theta})}{\mathrm{d}\theta}}\color{red}{\frac{\mathrm{d}\theta}{\mathrm{d}t}}, \color{blue}{\frac{\mathrm{d}(\sin{\theta})}{\mathrm{d}\theta}}\color{red}{\frac{\mathrm{d}\theta}{\mathrm{d}t}}\right)\\
&=&(\color{blue}{-}\color{red}{\dot{\theta}}\color{blue}{\sin{\theta}}, \color{red}{\dot{\theta}}\color{blue}{\cos{\theta}})\\
&=&\dot{\theta}(-\sin{\theta}, \cos{\theta})
\end{eqnarray}

したがって\((3)\)より、
\(\dot{\vec{e_r}}=\dot{\theta}\vec{e_{\theta}}\tag{4}\)
となります。

そして、\(\vec{e_{\theta}}\)を時間\(t\)で微分すると、(\((3)\)より、)

\begin{eqnarray}
\dot{\vec{e_{\theta}}}&=&\displaystyle\left(\frac{\mathrm{d}}{\mathrm{d}t}(-\sin{\theta}),\frac{\mathrm{d}}{\mathrm{d}t}(\cos{\theta})\right)\\
&=&\displaystyle\left(\color{blue}{\frac{\mathrm{d}(-\sin{\theta})}{\mathrm{d}\theta}}\color{red}{\frac{\mathrm{d}\theta}{\mathrm{d}t}}, \color{blue}{\frac{\mathrm{d}(\cos{\theta})}{\mathrm{d}\theta}}\color{red}{\frac{\mathrm{d}\theta}{\mathrm{d}t}}\right)\\
&=&(\color{blue}{-}\color{red}{\dot{\theta}}\color{blue}{\cos{\theta}}, \color{blue}{-}\color{red}{\dot{\theta}}\color{blue}{\sin{\theta}})\\
&=&-\dot{\theta}(\cos{\theta}, \sin{\theta})
\end{eqnarray}

したがって\((3)\)より、
\(\dot{\vec{e_{\theta}}}=-\dot{\theta}\vec{e_r}\tag{5}\)
となります。

\((4)\)と\((5)\)をふたたびまとめて書きます。

\begin{eqnarray}
\left\{
\begin{array}{l}
\dot{\vec{e_r}}=\dot{\theta}\vec{e_{\theta}}\\
\dot{\vec{e_{\theta}}}=-\dot{\theta}\vec{e_r}
\end{array}
\right.\tag{6}
\end{eqnarray}

\((6)\)をあとあと使っていきます。

極座標の速度、加速度を求める

さて、では下記の式

\(\vec{r}=r\vec{e_r}\tag{2}\)

を時間で微分することにより速度\(\vec{v}\)と加速度\(\vec{a}\)を求めていきます。
(注1: 式変形の途中で\(\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\)と「\(\dot{}\)」の両方が出てきますが、どちらでも意味は同じ (時間での微分) ですよ! 見やすさのため両方使っているだけです!)
(注2: 積の微分公式 \(\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}(a\vec{B})=\dot{a}\vec{B}+a\dot{\vec{B}}\) を使用します。スカラーとベクトルの積でもこの公式が成り立つんですよ。これについてもいつか記事を書きたい。)
(注3: 式\((6)\)を使うところを赤色にしておきますね。)

\begin{eqnarray}
\vec{v}&=&\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\\
&=&\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}(r\vec{e_r})\\
&=&\dot{r}\vec{e_r}+r\color{red}{\dot{\vec{e_r}}}\\
&=&\dot{r}\vec{e_r}+r\color{red}{\dot{\theta}\vec{e_{\theta}}}\tag{7}
\end{eqnarray}

ベクトル\(\vec{v}\)の\(r\)方向 (= \(\vec{e_r}\)の方向) の大きさが\(\dot{r}\)、\(\theta\)方向 (= \(\vec{e_{\theta}}\)の方向) の大きさが\(r\dot{\theta}\)ということですから、次のように表せます。

\begin{eqnarray}
\left\{
\begin{array}{l}
v_r=\dot{r}\\
v_{\theta}=r\dot{\theta}
\end{array}
\right.\tag{8}
\end{eqnarray}

式\((7)\)をもう1回微分して加速度\(\vec{a}\)を求めます。

\begin{eqnarray}
\vec{a}&=&\displaystyle\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\\
&=&\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}(\dot{r}\vec{e_r}+r\dot{\theta}\vec{e_{\theta}})\\
&=&\ddot{r}\vec{e_r}+\dot{r}\color{red}{\dot{\vec{e_r}}}+\dot{r}\dot{\theta}\vec{e_{\theta}}+r\ddot{\theta}\vec{e_{\theta}}+r\dot{\theta}\color{red}{\dot{\vec{e_{\theta}}}}\\
&=&\ddot{r}\vec{e_r}+\dot{r}\color{red}{\dot{\theta}\vec{e_{\theta}}}+\dot{r}\dot{\theta}\vec{e_{\theta}}+r\ddot{\theta}\vec{e_{\theta}}+r\dot{\theta}(\color{red}{-\dot{\theta}\vec{e_r}})\\
&=&(\ddot{r}-r\dot{\theta}^2)\vec{e_r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\vec{e_{\theta}}\tag{9}
\end{eqnarray}

ベクトル\(\vec{a}\)の\(r\)方向 (= \(\vec{e_r}\)の方向) の大きさが\(\ddot{r}-r\dot{\theta}^2\)、\(\theta\)方向 (= \(\vec{e_{\theta}}\)の方向) の大きさが\(2\dot{r}\dot{\theta}+r\ddot{\theta}\)ということですから、次のように表せます。

\begin{eqnarray}
\left\{
\begin{array}{l}
a_r=\ddot{r}-r\dot{\theta}^2\\
a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}
\end{array}
\right.\tag{10}
\end{eqnarray}

式\((8), (10)\)を再度並べて書きます。
\begin{eqnarray}
速度: \left\{
\begin{array}{l}
v_r=\dot{r}\\
v_{\theta}=r\dot{\theta}
\end{array}
\right.
\ \ \ \
加速度: \left\{
\begin{array}{l}
a_r=\ddot{r}-r\dot{\theta}^2\\
a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}
\end{array}
\right.
\end{eqnarray}

これで、公式\((1)\)を導くことができました!

もう1つ導き方があります

公式\((1)\)の導き方は実はもう1つあります。

よく知られた直交座標と極座標の変換公式
\((x, y)=(r\cos{\theta}, r\sin{\theta})\tag{11}\)
を微分していって、ところどころで極座標の基本ベクトルの表式
\begin{eqnarray}
\left\{
\begin{array}{l}
\vec{e_r}=(\cos{\theta}, \sin{\theta})\\
\vec{e_{\theta}}=(-\sin{\theta}, \cos{\theta})
\end{array}
\right.\tag{3}
\end{eqnarray}
を使う方法です。

式\((11)\)を時刻\(t\)で1回微分することにより、

\begin{eqnarray}
(v_x, v_y)&=&(\dot{r}\cos{\theta}-r\dot{\theta}\sin{\theta}, \dot{r}\sin{\theta}+r\dot{\theta}\cos{\theta})\tag{12}\\
&=&\dot{r}(\cos{\theta}, \sin{\theta})+r\dot{\theta}(-\sin{\theta}, \cos{\theta})
\end{eqnarray}
なので、\((3)\)より、
\begin{eqnarray}
\vec{v}=\dot{r}\vec{e_r}+r\dot{\theta}\vec{e_{\theta}}
\end{eqnarray}

ベクトル\(\vec{v}\)の\(r\)方向 (= \(\vec{e_r}\)の方向) の大きさが\(\dot{r}\)、\(\theta\)方向 (= \(\vec{e_{\theta}}\)の方向) の大きさが\(r\dot{\theta}\)ということですから、次のように表せます。

\begin{eqnarray}
\left\{
\begin{array}{l}
v_r=\dot{r}\\
v_{\theta}=r\dot{\theta}
\end{array}
\right.\tag{8}
\end{eqnarray}

さらに式\((12)\)を時刻\(t\)で1回微分することにより、

\begin{eqnarray}
(a_x, a_y)&=&(\ddot{r}\cos{\theta}-2\dot{r}\dot{\theta}\sin{\theta}-r\ddot{\theta}\sin{\theta}-r\dot{\theta}^2\cos{\theta}\\
&&\ \ \ \ , \ddot{r}\sin{\theta}+2\dot{r}\dot{\theta}\cos{\theta}+r\ddot{\theta}\cos{\theta}-r\dot{\theta}^2\sin{\theta})\\
&=&(\ddot{r}-r\dot{\theta}^2)(\cos{\theta}, \sin{\theta})+(2\dot{r}\dot{\theta}+r\ddot{\theta})(-\sin{\theta}, \cos{\theta})
\end{eqnarray}
なので、\((3)\)より、
\begin{eqnarray}
\vec{a}=(\ddot{r}-r\dot{\theta}^2)\vec{e_r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\vec{e_{\theta}}
\end{eqnarray}

ベクトル\(\vec{a}\)の\(r\)方向 (= \(\vec{e_r}\)の方向) の大きさが\(\ddot{r}-r\dot{\theta}^2\)、\(\theta\)方向 (= \(\vec{e_{\theta}}\)の方向) の大きさが\(2\dot{r}\dot{\theta}+r\ddot{\theta}\)ということですから、次のように表せます。

\begin{eqnarray}
\left\{
\begin{array}{l}
a_r=\ddot{r}-r\dot{\theta}^2\\
a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}
\end{array}
\right.\tag{10}
\end{eqnarray}

ぶじ、この方法でも\((8)\)と\((10)\)を導き出すことができました。

まあ、「フーン」くらいに思っておいてください。

極座標の速度･加速度はどんなふうに出てくるか

極座標の速度･加速度は物理学の勉強を進める中でどんなところでどんな風に出てくるのか軽く見てみましょう。

ブログ主の手持ちの教科書や参考書から抜粋してみたいと思います。

ここも「フーン」程度に思ってもらえれば十分です。
実際に出てきたときに「きた! あのやつね」と思ってもらえればしめたものです。

おそらく、大学学部レベルの物理学だと、①力学、②解析力学 の2科目で登場すると思います。

①力学

運動方程式の極座標表示
　質点に作用する力を\(r\)成分\(F_r\)と\(\theta\)成分\(F_{\theta}\)にわけると運動方程式は次のように書ける.
\begin{eqnarray}
\begin{array}{l}
m(\ddot{r}-r\dot{\theta}^2)=F_r\\
m\displaystyle\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}t}(r^2\dot{\theta})=F_{\theta}
\end{array}
\end{eqnarray}
質点に作用する力がつねに質点と原点を結ぶ直線上にある中心力の場合には\(F_{\theta}=0\)であるから\(\theta\)方向の運動方程式より次の結果を得る.
\begin{eqnarray}r^2\dot{\theta}=\mathrm{const.}\end{eqnarray}
左辺の量は面積速度の2倍であるから, この式は面積速度一定の原理に他ならない.

伊東敏雄 (1994年) 「な～るほど！の力学」より引用 (ブログ主がやや改変)

\(\ddot{r}-r\dot{\theta}^2\)は\(a_r\)のこと、
\(\displaystyle\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}t}(r^2\dot{\theta})\)は\(a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}\)を変形したものです。
(よかったら計算して確認してみてください。)

②解析力学

実はラグランジュ方程式では, \(\vec{v}(t)=(v_r, v_{\theta})\)までで十分なんだね。極座標表示されても, ラグランジアン\(L\)は\(L=T-U\)より, \(1\)質点の場合の\(L\)は,
\begin{eqnarray}
L&=&T-U=\displaystyle\frac{1}{2}m|\vec{v}|^2-U=\frac{1}{2}m({v_r}^2+{v_{\theta}}^2)-U\\
&=&\displaystyle\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-U
\end{eqnarray} と,
\(|\vec{v}|^2={v_r}^2+{v_{\theta}}^2\)だけから求めることができるからね。そして, これを次の自由度\(f=2\)のラグランジュの運動方程式に代入すればいいんだね。
\begin{eqnarray}
\displaystyle\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0,\ \ \ \ \ \ \ \displaystyle\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta}=0
\end{eqnarray}

馬場敬之 (2010年) 「スバラシク実力がつくと評判の 解析力学 キャンパス･ゼミ」より引用 (ブログ主がやや改変)

\(v_r=\dot{r}, v_{\theta}=r\dot{\theta}\)であることが使われていますね。

ここまでで、極座標の速度と加速度について、意味や求め方、教科書への登場のしかたの例などをひととおり説明しました。

極座標の速度と加速度が\((3)\)式のようになるいきさつを理解できたでしょうか。
そうだったらよいのですが。

まとめ

• 直交座標と極座標では、速度、加速度の表式が変わるというのが大事。具体的に表式を暗記することは大事ではない。
• 極座標の速度、加速度の表式を導く方法を知っておくことは有意義。
• 極座標の速度、加速度は、位置ベクトルを微分することで求めるが、その際、極座標の基本ベクトル\(\vec{e_r}, \vec{e_{\theta}}\)が時間に依存することに注意して式変形が必要である。
• 極座標の速度、加速度の表式は、力学と解析力学で登場する。