高校物理では「位置エネルギー」と呼ばれていたものが、大学物理では「ポテンシャルエネルギー」または、単に「ポテンシャル」と呼ばれます。
ポテンシャルは力学のみならず電磁気学、量子力学など物理学全般にわたって登場しまくる重要概念です。
あまりに頻繁に物理に出てくるので学生時代の私は、物理的なことを考えるときにポテンシャルというものはいつでも存在しているのだというイメージを何となく持っていました。
しかし教科書をちゃんと読めば「ポテンシャルが存在する条件」がしっかり書いてあります。つまりその条件に合致しない場合「= ポテンシャルが存在しない場合」も、たくさんあるのです。
その話の流れの中で「保存力」というワードが登場することになります。
今回の記事では、「ポテンシャルが存在する条件」と「保存力」という概念について、私なりの理解を解説します。あくまで私の理解です。
ポテンシャルエネルギーとは何か
ポテンシャル(= ポテンシャルエネルギー)とは、ひとことでいうと「位置エネルギー」です。
「位置エネルギー」については高校で習いますよね。
これを大学物理では「ポテンシャル(エネルギー)」とよぶ。ただそれだけの理解で大体大丈夫です。
(厳密さを求める詳しい方、ごめんなさい)
位置エネルギーについて高校の教科書では、以下のような説明がされていました。
重力による位置エネルギー 高く引き上げたおもりを落下させると,おもりは杭を打ちこむ仕事をする。おもりの質量が大きいほど,また,高さが高いほど,杭は深く打ちこまれる。一般に,高い所にある物体は,質量と高さに応じたエネルギーを蓄えている,と考えることができる。これを重力による位置エネルギーという。
数研出版 (2016年) 「改訂版 物理基礎」より引用
高いところから物体を落とすと、地面に近づくにつれて速度は大きくなります。
つまりざっくり言うと「高さ」が「速度」に変わったわけです。
言い換えると「位置エネルギー」が「運動エネルギー」に変わるわけです。
つまり「高い位置に物体がある」ということは「= 運動エネルギーを生み出す潜在的な活力を持っている」ということなのです。
「潜在的な活力」は英語にすると「potential energy (ポテンシャルエネルギー)」です。
だから 位置エネルギー = ポテンシャルエネルギー というわけです。
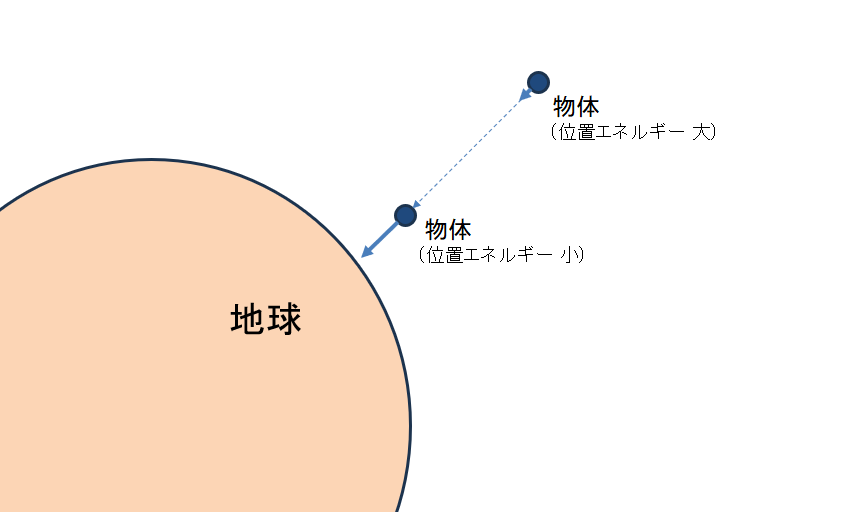
ポテンシャルエネルギーの近くにかならず力がある
ポテンシャルエネルギー (位置エネルギー) という言葉が教科書などで登場した時に、ひとつ知っておいてほしいことがあります。
それは、「ポテンシャルエネルギー (位置エネルギー) とセットになっている力があるはず」ということです。
上記の例では、「地球が物体を引きつける重力」が、ポテンシャルエネルギーとセットになっている”力”です。
ポテンシャルエネルギー は 力 の影のようなもの。
力 は ポテンシャルエネルギー のすぐ近くに常にある概念・存在だということを覚えておいてほしいです。
例を見てみましょう。
(前略)
杉山忠男 (2013年) 「わかる!できる!力がつく! カラー版 最強の力学入門」より引用
弾性力による位置エネルギー(弾性エネルギー)
ばねには自然長に戻ろうとする弾性力がはたらく。その弾性力は,ばねの伸び(あるいは縮み)を\(x\)とすると,\(-kx\)と表される。(中略) ばねに付けられた物体の弾性力による位置エネルギーを,単に,弾性エネルギーという。
「ばねの運動における位置エネルギー」 (現在は、くわしい意味がわからなくても大丈夫) と、「弾性力」という 力 がセットで登場していることがわかります。
電磁気学の教科書も見てみましょう。
力学の法則から,ポテンシャルエネルギー\(U\)をもつ物体には,\(U\)の負の勾配\(-\boldsymbol{\nabla}U\)によって与えられる力がはたらくことが導かれる.電位\(\phi\)の位置に置かれた点電荷\(q\)は\(U=q\phi\)のポテンシャルエネルギーをもち,電場\(\boldsymbol{E}\)から
\begin{equation}\boldsymbol{F}=q\boldsymbol{E}=-q\boldsymbol{\nabla}\phi=-\boldsymbol{\nabla} U\end{equation}
のローレンツ力を受けるというのが1つの例である.
水田智史 (2021年) 「プログレッシブ電磁気学 ーマクスウェル方程式からの展開ー」より引用
よくわからない単語や数式が出てきているかもしれませんが、「ポテンシャル」と「力」だけに注目して見てみてください。
「点電荷\(q\)がもつポテンシャルエネルギー」と、「ローレンツ力」(または、「\(U\)の負の勾配\(-\boldsymbol{\nabla}U\)によって与えられる力」)という 力 がセットで登場していることがわかります。
ポテンシャルが存在する力と存在しない力がある
「ポテンシャルエネルギーの存在のすぐ近くにかならず力があるはず」と上でいいました。
しかしその逆に、「力あるところにポテンシャルエネルギーはかならずあるのか?」
というと、実は…そうとは限りません。
これこそが、今回の記事でいちばん言いたいことです!
大事なことなのでもう1度言います。
ポテンシャルエネルギーはすべての力に存在するわけではありません。
つまりポテンシャルエネルギーが存在する力と、存在しない力があるのです。
このことだけ覚えて帰ってください。(何)
すると、ポテンシャルエネルギーが存在する力の条件を知りたいところです。
ポテンシャルエネルギーが存在する力とはどういう力なのでしょうか?
ここで「保存力」というワードが重要になってきます。
ポテンシャルが存在する力の条件
「保存力」というワードをまずは知りましょう。
「保存力」について教科書の説明を見てみます。
重力や摩擦力など,物体にはたらく力にはさまざまな力が存在するが,(中略) それらは,保存力 (conservative forces) と非保存力 (nonconservative forces) に分類することができる.保存力は,その力のもとで物体が2点間を移動する時,その力が物体にする仕事が始点と終点の位置だけで決まり途中の移動経路によらない力である.一方,非保存力は仕事が経路に依存する力である.
滝川昇, 新井敏一, 土屋俊二 (2018年) 「物理学基礎1 力学[入門編]」より引用
これをキュッとちぢめて言えば、以下のようになります。
- 「仕事が移動経路によらない力」 → 保存力という。
- 「仕事が移動経路による力」 → 非保存力という。
実は、ポテンシャルは保存力に対してのみ存在するものです。
非保存力にはポテンシャルというものはありません。
このことをしっかりと覚えてください!
ポテンシャルが存在しない力
さて、「仕事が移動経路による・よらない」とはどういうことでしょうか?
点Aから点Bに物体を移動させることを想像してみましょう。
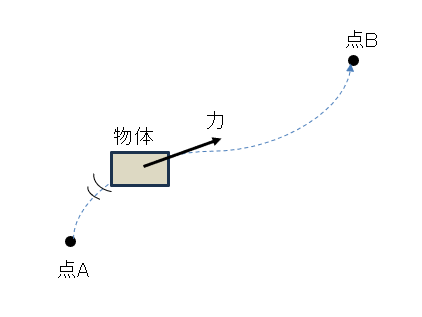
「仕事」とは、「物体に注ぎ込まれたエネルギー」のことだと思ってください。
点Aから点Bまで物体を動かす間に力を物体に継続してかける必要があるため、物体にエネルギーが注がれ続けていることになります。
この力によって注ぎ込まれたエネルギーの総量が「仕事」です。
ちなみにここでは深く考える必要はありませんが、仕事 (\(W\)とする) は、次の式で表されます。
\(W= \displaystyle \int^{B}_{A} \vec{F}( \vec{r} ) \cdot \mathrm{d} \vec{r} \tag{1} \)
(\(\vec{F}\)は物体にかける力、\(\vec{r}\)は物体の位置、\(\mathrm{d}\vec{r}\)は経路に沿った微小なベクトル素)
①人間が点Aから点Bまで物体を押して動かす場合
人間が物体を点Aから点Bまで押して動かすとした場合、点Aから点Bまでの間を一直線に押していけば、最も少ないエネルギーだけで運べそうです。
しかし、点Aから点Bまでの間にすごい遠回りをしたらどうでしょう。
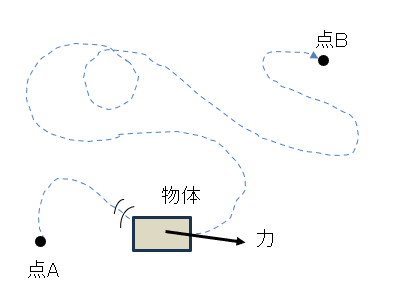
直線的に運ぶよりも、明らかにエネルギーをたくさん使うことが想像されると思います。
つまり、直線的な経路で運ぶのと遠回りな経路で運ぶのとでは使うエネルギー量(= 仕事)が違います。
これを知的っぽい言い方をすると、「仕事が移動経路による」(移動経路によって変わる)ということになります。
つまり「人間が物体を押す力」は保存力ではありません。
なのでこのような力にポテンシャルは存在しません。
ポテンシャルが存在する力
では、点Aから点Bまでの間、重力を利用して物体を運ぶ場合はどうでしょうか。
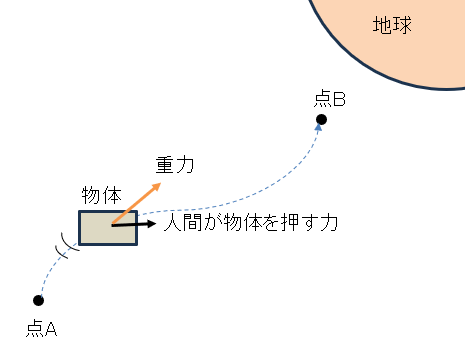
(人間がかける力は置いておいて)「重力が物体にする仕事」を考えてみましょう。
地球は、物体が右に遠回りして点Bまで移動しようと、左に遠回りして点Bまで移動しようと、「地球に物体を近づける方向の力」のみを物体に及ぼします。
物体が地球に近づく時以外には、地球はエネルギーを消費しません。
結果的に、どんな経路をたどったとしても地球は下図の「点Aの高さ」から「点Bの高さ」まで物体を近づけるだけのエネルギーしか物体に注ぎ込みません。
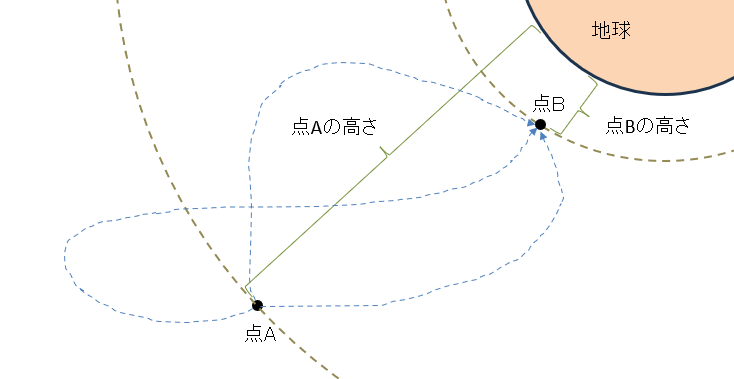
もし、物体が点Aから逆方向に進んだ時、重力は「負のエネルギー消費をしている」とお考え下さい。
結果的に、点Bまでの間に重力がする仕事は「『点Aの高さ』から『点Bの高さ』まで物体を近づけるエネルギー」と同じ一定の量であり、どの経路でも同じです。
これを知的っぽい言い方をすると、「仕事が移動経路によらない」(移動経路によって変わらない)となります。
つまり「重力」は保存力です。
なので重力には位置エネルギーが定義でき、つまりポテンシャルが存在します。
保存力、非保存力 の例
保存力と非保存力の区別がわかったところで、では、保存力にはどんな例があるのか? 非保存力にはどんな例があるのか? を挙げてみましょう。
よく教科書で挙げられているものは下記のようになります。
- 保存力の例: 重力、ばねの弾性力、電気力、磁気力、浮力 など
- 非保存力の例: 摩擦力、空気抵抗力、粘性抵抗力 など
上記の保存力には、ポテンシャルを定義できます。
上記の非保存力には、ポテンシャルを定義することができません。
ポテンシャルが存在しない力ということです。
身の周りの力を探してみて、それが保存力か、非保存力か、調べたり考えたりしてみると面白いかもしれません。
「保存力」というネーミングについて
ある力が保存力の場合には、ポテンシャルエネルギーが定義できることを学びました。
保存力の定義は「仕事が移動経路によらない力」です。
どの教科書を見ても、「保存力とは、仕事が移動経路によらない力である」という説明が書いてあると思います。これは正しい説明です。
しかし、「保存力」という用語のネーミングから考えると、「仕事が移動経路によらない力」という説明ではなく、保存力とは「○○が保存する力」であると言ってほしいものです!
現実問題、保存力では何が保存するのでしょうか?
保存力において保存されるもの、それは「力学的エネルギー」です。
力学的エネルギーは高校物理で習うのでみんな知っているはずです。
運動エネルギー\(K\)と位置エネルギー\(U\)の和\(E=K+U\)を力学的エネルギーという。
数研出版 (2016年) 「改訂版 物理基礎」より引用
上記の教科書にも書いてあるとおり、力学的エネルギーとは、運動エネルギーとポテンシャル (= 位置エネルギー) の和のことです。
これが保存力では常に保存するから、保存力というネーミングになっている。
じゃあ、保存力の定義は「力学的エネルギーが保存する力」でいいじゃん。と思えます。
しかしそれでは駄目です。なぜなら、上記から分かるように、力学的エネルギーはポテンシャルが存在している場合のみ定義できる物です。
そしてポテンシャルは力が保存力の場合のみ定義できる物です。
ここで保存力の定義を「力学的エネルギーが保存する力」としてしまうと、
力学的エネルギー → ポテンシャル → 保存力 → 力学的エネルギー → …
というように定義が循環してしまいます。これでは論理的に正しい定義と言えません。
だから、保存力の定義は「仕事が移動経路によらない力」という、力学的エネルギーを含まない定義にしなくてはならなかったのだと思われます。
しかし、「保存力」といわず「ポテンシャル存在力」(ポテンシャルが存在する力という意味)とでもいうネーミングにしておけば、少しは分かりやすかったんじゃないかな、と思います。
とはいえ「ポテンシャル存在力」より「保存力」のほうがだんぜん短くて言いやすい言葉です。
短くて言いやすいのもすごく大事です。だから最終的に「保存力」というネーミングになったのでしょうと思います。
(ブログ主はプログラミングをする人間なので、ネーミングの簡潔さの重要性は痛いほどわかる)
「保存力」というネーミングは、まあ、無難な落としどころということでしょう。
あまり愚痴を言ってもしかたないので、初学者の人も慣れていくようにしたい所です。
最後に例題
次の文章の間違っている点を見つけ、正しい文章に言い直してください。
(1) どんな力にもポテンシャルエネルギーが存在する。そのため重力、電気力、摩擦力、空気抵抗力 にはどれもポテンシャルエネルギーを定義することができる。
(2) 保存力の定義は「力学的エネルギーが保存する力」である。
(3) 物体に地球の重力がはたらいている状況で、物体をある点からある点へ移動させるとき、遠回りすればするほど、重力がする仕事は大きくなる。
まとめ
- ポテンシャル(エネルギー)とは、高校で習った位置エネルギーのことである。
- 仕事とは、物体が移動したとき、力によって物体に注ぎ込まれたエネルギーのことである。
- ポテンシャルは、力が保存力の場合にのみ存在する。
- 保存力とは、「仕事が移動経路によらない力」である。
- 保存力の例は、重力、ばねの弾性力、電気力、磁気力、浮力。
非保存力の例は、摩擦力、空気抵抗力、粘性抵抗力。 - 保存力の定義を「力学的エネルギーが保存する力」とすると定義が循環してしまうので、そういう定義にはなっていないのだと思われる。
以上です。読んでくれてありがとうございました。



コメント